Effect of latent space distribution on the segmentation of images with multiple annotations

Bhat, Ishaan; Pluim, Josien P.W.; Viergever, Max A.; Kuijf, Hugo J.

doi:https://doi.org/10.59275/j.melba.2023-18ae

1 Introduction

Image segmentation may be posed as a supervised classification task with a deep learning system trained using manually created rater labels, producing a segmentation map by estimating per-voxel class probabilities. A shortcoming of standard deep learning approaches is that they produce point estimate predictions and not an output distribution from which multiple plausible predictions can be sampled (Kendall and Gal, 2017). This disadvantage is highlighted when multiple segmentations per image are available, which standard deep learning approaches cannot leverage. Inter-rater variability reflects the disagreement among raters and ambiguity present in the image, and ideally, a supervised learning approach needs to reflect this uncertainty for unseen test cases (Jungo et al., 2018).

The uncertainty present in a prediction can be decomposed into uncertainty originating from the model (epistemic) and uncertainty originating from the data (aleatoric) (Armen Der Kiureghian and Ditlevsen, 2009). Epistemic uncertainty can be reduced by making more data available to train a classifier, but aleatoric uncertainty is irreducible (Kendall and Gal, 2017). Bayesian techniques to estimate epistemic uncertainty in deep learning models usually involve producing multiple outputs by sampling model parameters from an approximating distribution (Gal and Ghahramani, 2016; Blundell et al., 2015; Kingma et al., 2015; Teye et al., 2018). The most popular among these, MC-Dropout (Gal and Ghahramani, 2016), estimates pixel-wise uncertainty using dropout (Srivastava et al., 2014) to sample model parameters over multiple passes. Where multiple segmentations are available, it has been shown that regions of high estimated uncertainty reflect human disagreement (Jungo et al., 2018; Chotzoglou and Kainz, 2019; Jensen et al., 2019). While this technique is sufficient to produce good pixel-wise uncertainty estimations, it may produce spatially inconsistent segmentations (Kohl et al., 2018).

Techniques that are not explicitly Bayesian in nature, like model ensembles (Lakshminarayanan et al., 2017), have been a popular choice to obtain good quality segmentations and well-calibrated epistemic uncertainty estimates (Kamnitsas et al., 2018; Mehrtash et al., 2020). However, training a model ensemble has a large computational overhead. In Rupprecht et al. (2017) the authors propose a network architecture with multiple outputs (or M-Heads) that share a common backbone network, which can mimic an ensemble with a lower compute footprint. Thus, the model ensemble and M-Heads are not scalable because the number of models (or M-Heads) are fixed during training. Furthermore, the outputs produced by ensembles may be unable to capture the diversity in the reference segmentations and fail to produce rare variants in the output distribution (Kohl et al., 2018).

Techniques that estimate aleatoric uncertainty use an approximating distribution for the input (Wang et al., 2019), output (Kendall and Gal, 2017; Monteiro et al., 2020), or intermediate layers (latent space) (Sohn et al., 2015; Kohl et al., 2018). Samples drawn from this approximating distribution are used to quantify the uncertainty.

Test-time augmentation (TTA) (Wang et al., 2019) is an uncertainty estimation technique that estimates aleatoric uncertainty by generating multiple plausible outputs using transformed versions of the input. In Kendall and Gal (2017) the authors induce a Gaussian distribution over the output feature map and estimate the mean and standard deviation for each logit. Since there is no correlation between pixels, the samples produced are not realistic and the quantified uncertainty is poor (Jungo et al., 2020). To address this short-coming, Monteiro et al. (2020) use a Gaussian distribution with a low-rank parameterization of the covariance matrix to model the joint distribution over the output logits, to produce diverse and plausible outputs.

In Kohl et al. (2018) the authors combine the conditional variational autoencoder (Sohn et al., 2015) framework with the popular U-Net (Ronneberger et al., 2015) architecture to create the Probabilistic U-Net to estimate aleatoric uncertainty by leveraging labels from multiple annotators. Different plausible variants of the prediction are computed by sampling from the (learned) latent space and combining this sample with the highest resolution feature map of the U-Net.

In Hu et al. (2019) the authors extend the Probabilistic U-Net to capture epistemic uncertainty by using variational dropout (Kingma et al., 2015) over the model weights. The PHISegNet (Baumgartner et al., 2019) shows a further improvement in sample diversity by using a series of hierarchical latent spaces from which samples are combined with the U-Net feature maps at different resolutions.

The Probabilistic U-Net and its hierarchical variants use an axis-aligned Gaussian distribution to model the distribution over the latent space. However, techniques such as normalizing flows (Rezende and Mohamed, 2015), which convert simple distributions into complex ones via invertible transformations, have been shown to be a promising alternative to model the latent space distribution (Selvan et al., 2020).

Given the success of the Probabilistic U-Net (and its hierarchical variants) at estimating the aleatoric uncertainty (Kohl et al., 2018; Baumgartner et al., 2019), and the improvement shown by methods using more complex distributions to approximate the distribution over the latent space (Selvan et al., 2020), we propose the Generalized Probabilistic U-Net that can use more general forms of the Gaussian distribution to model the latent space distribution to better approximate the uncertainty in the reference segmentations.

In this paper, we extend our previous work (Bhat et al., 2022) with the following additions:

•
Inclusion of an additional dataset of white matter hyperintensities in the brain (Kuijf et al., 2019)
•
Estimation of the covariance matrix of the latent space distribution using a low-rank factor matrix (Section 2.2.2)
•
Inclusion of popular uncertainty estimation techniques and additional experiments (Section 3.3)

Section 2 provides background on variational inference (Section 2.1) and describes our additions to the Probabilistic U-Net framework to allow more general forms of the Gaussian distribution to be used as the latent space distribution (Section 2.2). Section 3 describes the datasets used (Section 3.1), neural network training (Section 3.2), and the evaluation metrics used to quantify performance (Section 3.3). In Section 4, we present our results and discuss their implications.

2 Methods

2.1 Background

Variational inference (VI) (Wainwright and Jordan, 2007) is a tool to approximate complex probability distributions in a scalable and computationally efficient manner. Variational autoencoders (VAEs) (Kingma and Welling, 2014; Rezende et al., 2014), a class of deep latent variable models, were developed to perform generative modelling with possible one-to-many mappings. They do so by learning a distribution over the latent variables using variational inference, and sample from this distribution to generate multiple plausible outputs. In Sohn et al. (2015) the authors created a conditional variant (cVAE) to handle structured prediction problems like image segmentation.

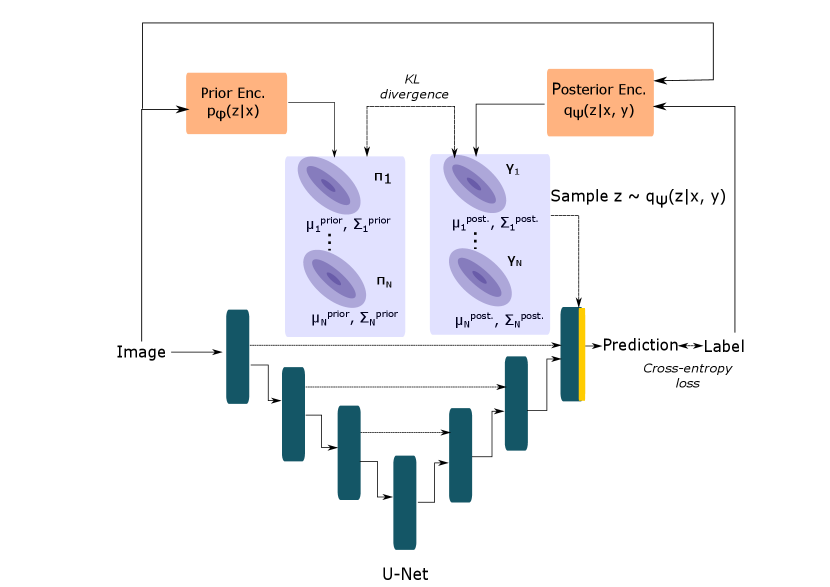
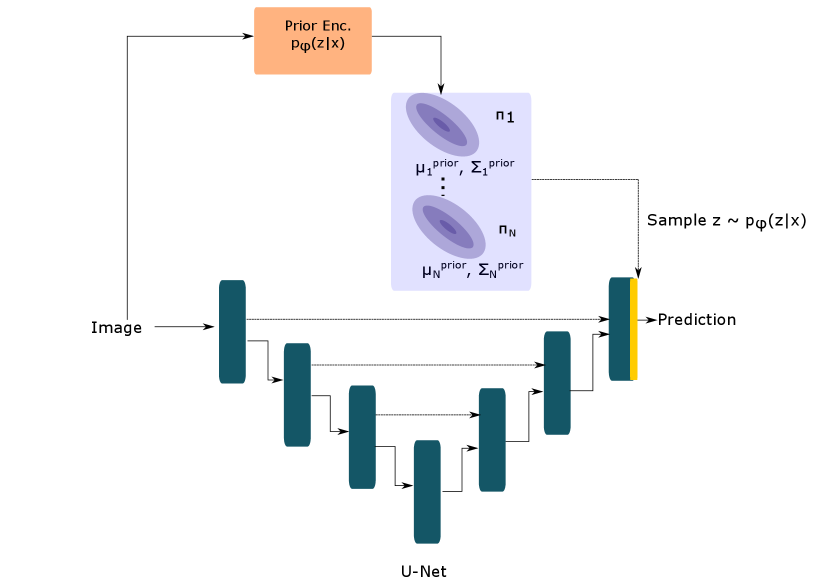
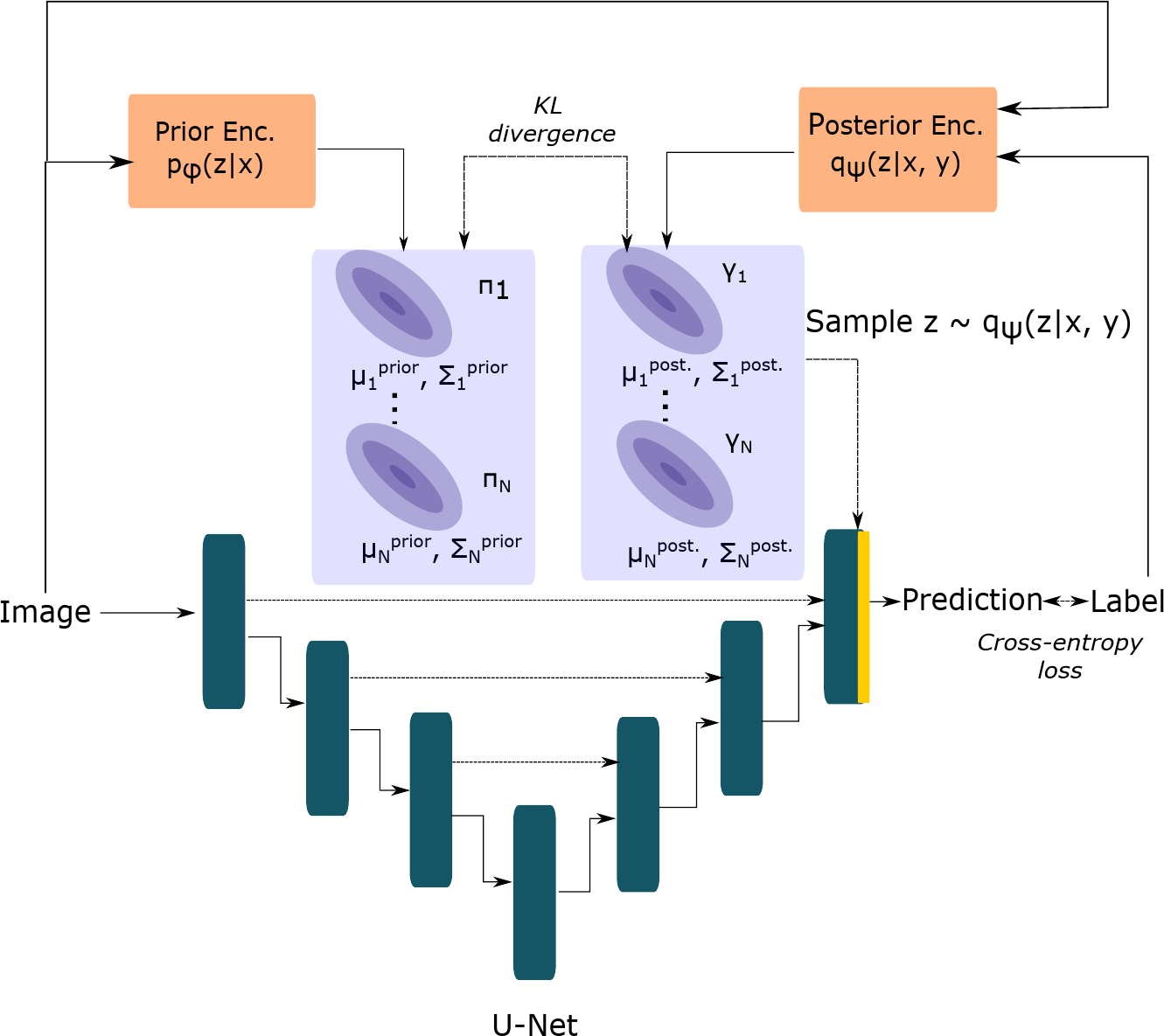
In a medical image segmentation problem, we typically have an image $x\in\mathbb{R}^{H\times W}$ and label $y\in\{0,1\}^{H\times W}$ and the goal is to produce accurate and coherent samples from the distribution $p_{\theta}(y|x)$ using a deep neural network parameterized by $\theta$ . To enable tractable sampling from $p_{\theta}(y|x)$ , simple distributions $p_{\phi}(z|x)$ and $q_{\psi}(z|x,y)$ are used as approximations for the true prior and posterior distributions over the latent space respectively. The distributional parameters for $q_{\psi}(z|x,y)$ and $p_{\phi}(z|x)$ are learnt by neural (sub-)networks parameterized by $\psi$ and $\phi$ respectively.

The training objective for the cVAE is minimizing the KL-divergence between the true and approximating posterior distributions (Sohn et al., 2015):

\mathbb{L}_{Tr}(\theta,\phi,\psi;x,y)=-\mathbb{E}_{q_{\psi}(z|x,y)}[\mathrm{log}\,p_{\theta}(y|x,z)]+\beta*\mathrm{KL}(q_{\psi}(z|x,y)||p_{\phi}(z|x))

(1)

In Equation 1, the first term is the expected value of the standard cross-entropy loss computed under the posterior distribution. The second term is the Kullback-Leibler (KL) divergence between the prior distribution, $p_{\phi}(z|x)$ , and the posterior distribution, $q_{\psi}(z|x,y)$ . This term acts as a regularization term that pulls the prior and posterior distribution closer to each other by penalizing their differences (Kohl et al., 2018). This is desirable since the posterior network is discarded during test-time. The $\beta$ term controls the trade-off between the segmentation and KL-loss terms (Higgins et al., 2017).

The reparameterization trick (Kingma and Welling, 2014) is used to generate samples from $q_{\psi}(z|x,y)$ in a computationally efficient manner. This trick is used to obtain an unbiased estimate of the gradient of the expectation term $\mathbb{E}_{q_{\psi}(z|x,y)}[\mathrm{log}\,p_{\theta}(y|x,z)]$ and make it differentiable with respect to parameters $\psi$ . Therefore, it is convenient if the distribution chosen to approximate the latent space distribution supports the reparameterization trick.

2.2 Contributions

The cVAE (Sohn et al., 2015) uses an axis-aligned Gaussian to model the prior and posterior distributions over the latent space. The Probabilistic U-Net (Kohl et al., 2018) combines the VI framework of the cVAE with the U-Net (Ronneberger et al., 2015) architecture. Additionally, it makes output computation efficient by merging the sample from the latent space distribution at the last layer of the U-Net.

We propose three extensions to this framework by using more general forms of the Gaussian distribution as choices for the latent space distributions in order to better capture the uncertainty in the reference segementations. Our generalized Probabilistic U-Net framework is shown in Figure 1.

2.2.1 Full-covariance Gaussian

For a matrix to be a valid covariance matrix, it must be positive semi-definite. Since this constraint is difficult to impose while training a neural network, the covariance matrix $\Sigma$ is built using its Cholesky decomposition $L$ (Williams, 1996):

\Sigma=LL^{T}

The matrix $L$ is a lower-triangular matrix with a positive-valued diagonal. By masking the upper-triangular section of the matrix and using the exponential operator to ensure positive values on the diagonal, $L$ can be directly computed by the neural network. Samples can be drawn from the full-covariance Gaussian using the reparameterization trick (Kingma and Welling, 2019):

\displaystyle z=\mu+L*\epsilon,\ \epsilon\sim\mathcal{N}(0,I)

2.2.2 Full-covariance Gaussian with a low-rank parameterization

A limiting factor in modelling a Gaussian with a full covariance matrix using neural networks is often the squared dependence between the size of the covariance matrix and dimensionality of the random variable. In Barber and Bishop (1997) the authors use a low-rank factor matrix $P$ and a diagonal matrix $D$ to build the covariance matrix used to model the posterior distribution over the neural network weights. We use this technique to build the covariance matrix $\Sigma$ for our latent space distribution:

\Sigma=PP^{T}+D

For a $N$ -dimensional Gaussian distribution, $D$ is a $N$ -dimensional vector with the diagonal elements and $P$ is a $N\times R$ factor matrix, where $R$ is a hyperparameter that defines the rank of the parameterization. The $P$ and $D$ matrices are computed as outputs of the posterior and prior encoders. This low-rank parameterization also supports the reparameterization trick for sampling via the Cholesky decomposition of $\Sigma$ (Monteiro et al., 2020).

2.2.3 Modelling of mixture of Gaussians

Any arbitrary (continuous) distribution can be modelled by a mixture of a sufficient number of Gaussians, with appropriate mixture weights (Bishop, 2006). Mixtures of Gaussians have been used to model posterior distributions in variational autoencoders for clustering tasks (Jiang et al., 2017; Kopf et al., 2021).

For example, the posterior distribution¹¹1This subsection holds true for the cVAE prior distribution as well. The only difference is the dependence on the label, $y$ , is dropped. $q_{\psi}(z|x,y)$ can be modelled as a mixture of $N$ Gaussians as follows:

q_{\psi}(z|x,y)=\sum_{i=1}^{N}\gamma_{i}\mathcal{N}(\mu_{i}(x,y),\Sigma_{i}(x,y))

The individual Gaussians in the mixture, $\mathcal{N}(\mu_{i}(x,y),\Sigma_{i}(x,y))$ , are called the component distributions and the weights for the component distributions, $\{\gamma_{i}\}_{i=1}^{N}$ , are the mixing coefficients. The individual Gaussians can be modelled using a diagonal or full covariance matrix. For the distribution to be valid, the mixing coefficients must be greater than or equal to $0$ and sum to $1$ . Therefore, a categorical distribution can be used to define the mixture distribution.

As explained in Section 2.1, a distribution chosen to model the posterior must support differentiable sampling. To sample from a mixture of Gaussians, a component index is sampled from the categorical distribution defined by the mixture coefficients and then a value is sampled from the corresponding component (Gaussian) distribution.

	$\displaystyle i\sim\mathrm{Cat}(N;\gamma)$
	$\displaystyle z\sim\mathcal{N}(\mu_{i}(x,y),\Sigma_{i}(x,y))$

The second step in the sampling process is differentiable and supports the reparameterization trick, however, the first step, that is, sampling from a categorical distribution is not differentiable. To make sampling fully differentiable, we used the Gumbel-Softmax (GS) distribution(Jang et al., 2017; Maddison et al., 2017) to model the mixture distribution. The Gumbel-Softmax distribution is a continuous relaxation (defined by the temperature parameter, $\tau$ ) of the discrete categorical distribution, that supports differentiable sampling via the reparameterization trick. To obtain a discrete component index, we perform Straight-Through(ST) sampling (Jang et al., 2017), where we used the $\mathrm{argmax}$ operation in the forward pass and used the continuous relaxation in the backward pass while computing gradients used to update model parameters during training. With this, we used the following two-step process to sample from the mixture of Gaussians:

	$\displaystyle i\sim\mathrm{GS}(N;\gamma,\tau)$
	$\displaystyle z\sim\mathcal{N}(\mu_{i}(x,y),\Sigma_{i}(x,y))$

Unlike for a pair of Gaussians, the KL divergence for a pair of Gaussian mixtures does not have a closed-form expression. We estimated the KL divergence in Equation 1 via Monte Carlo sampling, which provides a good approximation (Hershey and Olsen, 2007).

Table 1: Neural network hyperparameters for LIDC-IDRI and WMH datasets. The number of U-Net encoder and decoder blocks were fixed at

3

, and the filter depths used were

32,64,128

for the first, second and third blocks respectively. The bottleneck layer had a filter depth of

512

. The numbers below each of the hyperparameters indicate the search space, with square brackets indicating a full grid search among the values between parenthesis, and curved brackets indicating random sampling in the range of values between parenthesis.

Model	Hyper-parameters (LIDC-IDRI / WMH)
	Latent space dimension	$\beta$	Rank	Mixture components	Temperature	Dropout rate
	$[2,4,6,8]$	$[1,10,100]$	$[1,7]$	$(1,10)$	$(0.1,0.5)$	$[0.1,0.3,0.5]$
AA	6 / 4	1 / 1	- / -	- / -	- / -	- / -
FC	2 / 2	1 / 1	- / -	- / -	- / -	- / -
FC-LR	2 / 2	1 / 1	1 / 1	-/-	- / -	- / -
AA Mixture	4 / 4	1 / 1	-	5 / 3	0.36 / 0.20	- / -
FC Mixture	2 / 4	1 / 1	-	9 / 4	0.28 / 0.22	- / -
FC-LR Mixture	4 / 8	1 / 1	2 / 7	2 / 9	0.20 / 0.17	- / -
MC-Dropout	- / -	- / -	- / -	- / -	- / -	0.3 / 0.3

3 Experiments

3.1 Data

3.1.1 LIDC-IDRI

The LIDC-IDRI dataset (Armato et al., 2011) consists of $1018$ thoracic CT scans with lesion segmentations from four raters. Like Kohl et al. (2018) and Baumgartner et al. (2019), we use a pre-processed version of the dataset, consisting of $128\times 128$ patches containing lesions.

We obtained a total of $15,096$ patches. We used a $60:20:20$ split to randomly partition the dataset into $9058,\,3019,$ and $3019$ patches for training, validation, and test respectively. The intensity of the patches was scaled to $[0,1]$ range and no data augmentation was used. We used the publicly available version of the pre-processed dataset from https://github.com/stefanknegt/Probabilistic-Unet-Pytorch.

3.1.2 White matter hyperintensities (WMH)

The WMH dataset (Kuijf et al., 2019) consists of $60$ MR images collected from three centers: University Medical Center (UMC) Utrecht ( $20$ patients), VU University Medical Center (VU) Amsterdam ( $20$ patients), both in the Netherlands, and the National University Health System (NUHS) ( $20$ patients) in Singapore.

For each patient, a 3D T1-weighted and a 2D multi-slice FLAIR image were provided. For each patient, the 3D T1-weighted image was registered to the FLAIR image using the elastix (Klein et al., 2010) toolbox to create a two-channel image. A brain mask was created from the FLAIR image using the ROBEX (Iglesias et al., 2011) technique, which was applied to the T1-weighted image as well. All $60$ images had white matter hyperintensities annotated by three raters.

We used a $80:10:10$ split to get $48,\,6$ , and $6$ patients for training, validation, and test respectively. From each patient MR image, we only used slices that have at least one non-empty segmentation. All images and labels were padded to be $256\times 256$ in dimension. Each image was normalized using the (channel-wise) mean and standard deviation. During training, we used random flips, random rotation, contrast, and brightness manipulation to perform data augmentation.

3.2 Neural network training

For all datasets and models, we used the ADAM (Kingma and Ba, 2015) optimizer with a learning rate of $10^{-4}$ . Training was stopped when the validation loss did not improve for more than 20 epochs, and the model parameters with the minimum validation loss were saved. During each iteration, random sampling was performed to select a rater and the corresponding ground truth segmentation was chosen to calculate the training loss and perform parameter updates. We chose hyperparameters for both datasets and the different configurations of the Generalized Probabilistic U-Net via a random grid search strategy. The hyperparameters for all datasets and models are shown in Table 1.

To ensure comparability between models with different latent space distributions, we maintain the same number of layers for the U-Net, the prior encoder, and the posterior encoder. Furthermore, in accordance with the original Probabilistic U-Net architecture, the prior and posterior encoder have the same architecture as the U-Net encoder. Each convolution block in the model consisted of convolution with a $3\times 3$ kernel, a ReLU nonlinearity and batch normalization (Ioffe and Szegedy, 2015). Downsampling is performed via average pooling and upsampling is performed via bilinear interpolation.

The code for the neural network training and inference was developed using the PyTorch (Paszke et al., 2019) library.

3.3 Evaluation

We study different configurations of the Generalized Probabilistic U-Net by using different distributions (Section 2.2) to model the latent space distributions. Additionally, we included the popular uncertainty estimation techniques MC-Dropout (Gal and Ghahramani, 2016) and model ensembles (Lakshminarayanan et al., 2017). We included the following models in our experiments:

•
Axis-aligned Probabilistic U-Net (AA) (Kohl et al., 2018)
•
Full covariance Probabilistic U-Net (FC)
•
Full covariance Probabilistic U-Net [Low-rank parameterization] (FC-LR)
•
Mixture AA Probabilistic U-Net
•
Mixture FC Probabilistic U-Net
•
Mixture FC-LR Probabilistic U-Net
•
MC-Dropout (Gal and Ghahramani, 2016)
•
Model ensemble (Lakshminarayanan et al., 2017)

To ensure a fair comparison between the Generalized Probabilistic U-Net configurations and the rest, MC-Dropout and model ensemble used the same U-Net architecture as the Probabilistic U-Net variants. The model ensemble was created by training $16$ models independently using different random seeds. The dropout rate for the MC-Dropout model was selected based on minimum validation loss. The dropout rate chosen for the WMH and LIDC-IDRI datasets was $0.3$ .

We used the generalized energy distance (GED) metric (Kohl et al., 2018) to compare how well the distribution of neural network predictions $P_{s}$ matched the distribution of ground truth labels $P_{gt}$ .

D^{2}_{GED}(P_{gt},P_{s})=2\mathbb{E}[d(S,Y)]-\mathbb{E}[d(S,S^{\prime})]\\ -\mathbb{E}[d(Y,Y^{\prime})]

(2)

The distance metric between a pair of segmentations, $d(x,y)$ , is defined as $1-\mathrm{IoU}(x,y)$ (Kohl et al., 2018; Baumgartner et al., 2019). In Equation 2, $S,S^{\prime}$ are samples from the prediction distribution and $Y,Y^{\prime}$ are samples from the ground truth distribution. The expectation terms in Equation 2 are computed via Monte Carlo estimation. We used $16$ samples from the prediction distribution to compute the GED. A lower GED implies a better match between prediction and ground truth distributions.

We also studied the trends in the component terms of the GED metric. The first term $\mathbb{E}[d(S,Y)]$ signifies the extent of overlap between samples from the prediction and ground truth distribution, while the second term $\mathbb{E}[d(S,S^{\prime})]$ is the sample diversity in the predictions. As a baseline for the overlap trends, we included results obtained on the test-set using a single U-Net (Ronneberger et al., 2015). To provide context for the sample diversity in the predictions, we included the diversity in the labels in our results. By investigating the correlation of these terms with the GED metric, we studied the interplay between overlap and diversity that lead to a better (or worse) match between distributions.

To study the effect the choice of latent space distribution has on capturing uncertainty, we partitioned the test-set of the LIDC-IDRI dataset into four subsets, based on rater agreement. The slices were assigned to one of the four subsets based on the number of raters (1-4) that annotated a lesion in it.

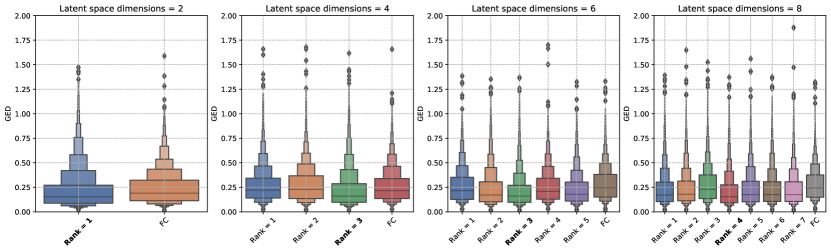
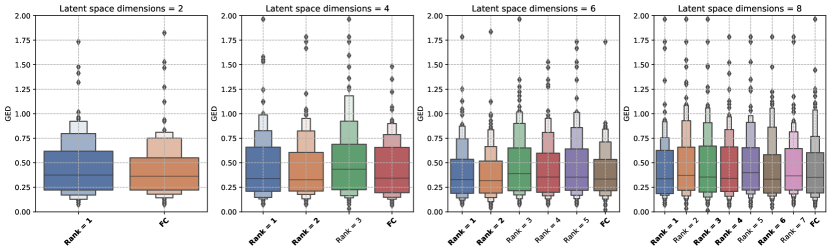
We studied the influence of the rank (number of columns in $P$ ) hyperparameter used to construct the covariance matrix for the FC-LR configuration of the Generalized Probabilistic U-Net. For each of the latent space dimensions in the hyperparameter search space (Table 1), we analysed the trends in the GED for the allowed values of the rank.

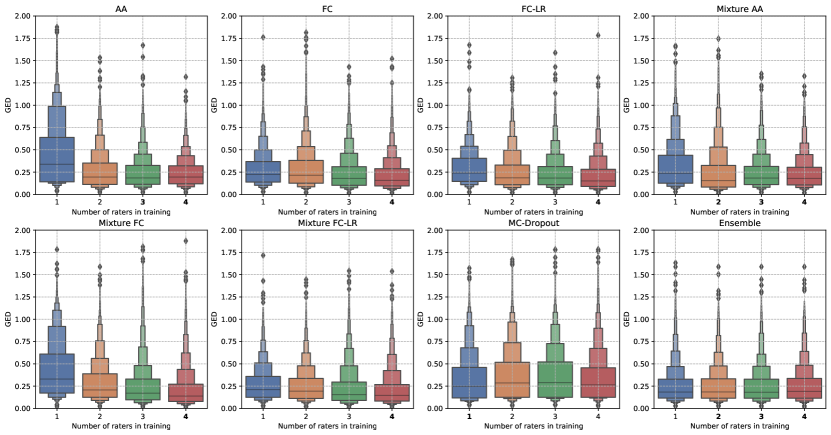
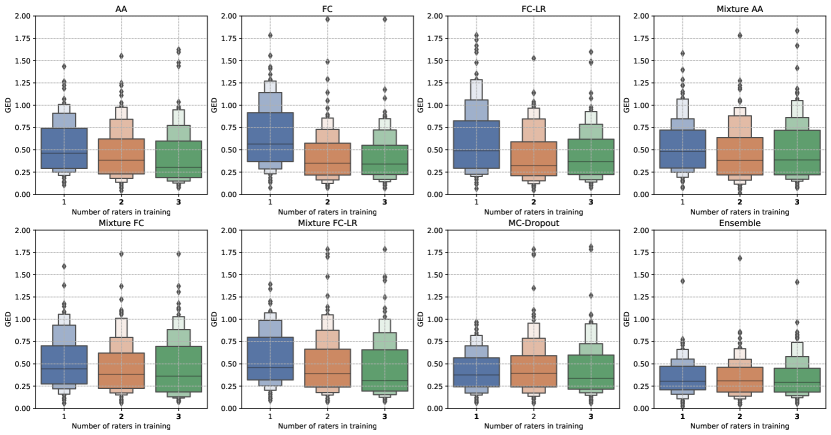
Lastly, we studied the effect the number of raters has on the ability of the model to predictions that accurately match the ground truth distribution. To do so, we trained each model on a sub-set of raters and evaluated their performance using segmentations from all the raters.

To check for statistical significance of differences in the metrics for models, we performed the Wilcoxon signed-rank test at a significance of $0.05$ .

4 Results and Discussion

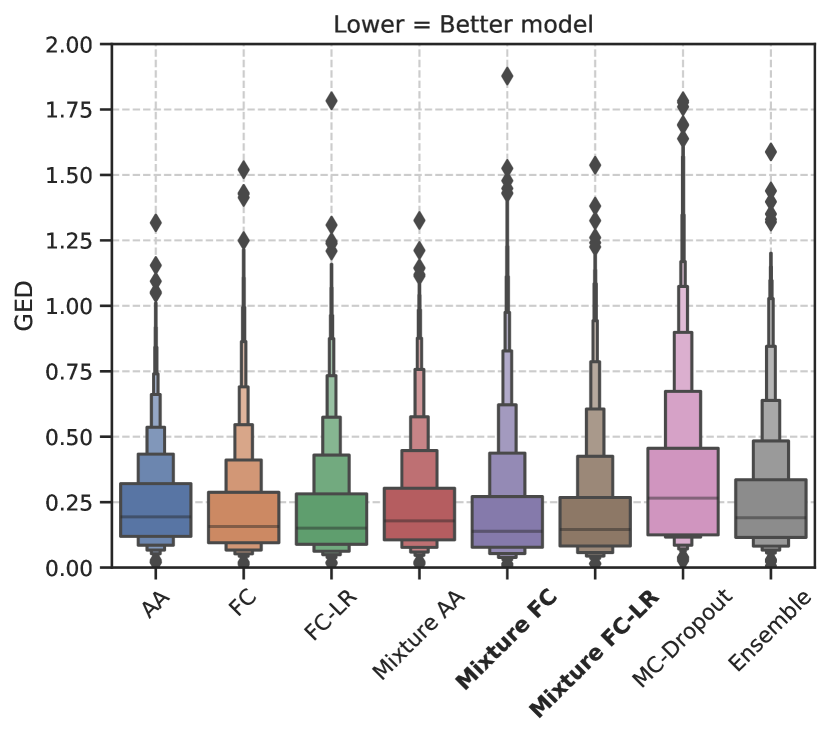
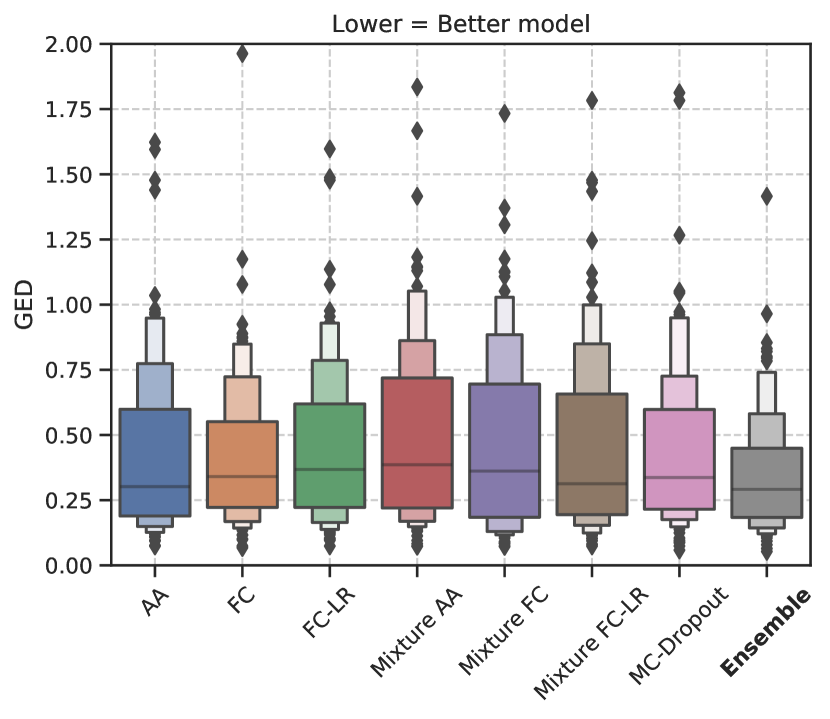
Figure 2 shows the trend in the GED metric for both datasets. The results show that the optimal choice of model, with respect to the median GED, depends on the dataset. In Figure 2(a), we see that the models using a mixture of Gaussians to model the latent space distribution (Mixture FC and Mixure FC-LR) perform best with respect to GED for the LIDC-IDRI dataset. In Figure 2(b), the model ensemble performs best for the WMH dataset.

Furthermore, we see that the different configurations of the Generalized Probabilistic U-Net do considerably better than MC-Dropout/model ensemble for the LIDC-IDRI dataset. For the WMH dataset, we observed very similar performances by all the models studied. The GED results showed that there was no statistically significant difference between any model pair except the model ensemble.

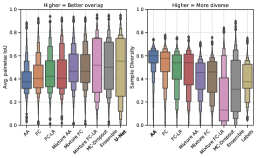
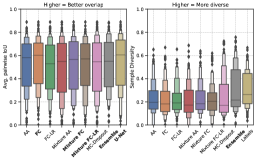
To explain model performances in Figure 2, we studied trends in overlap and diversity terms in the GED equation (Equation 2), shown in Figure 3. A model that produces predictions that have a higher overlap capture the common variants, whereas predictions with a higher diversity can capture rarer variants in the output distribution. Therefore, the GED, which essentially captures the distance between distributions, is determined by the balance between diversity and overlap.

In Figure 3(a), for the LIDC-IDRI dataset, we show that the Generalized Probabilistic U-Net configurations have a lower average overlap, but higher diversity compared with the MC-Dropout, ensemble, and U-Net models. Therefore, these models capture the common outcome well, but fail to produce diverse outputs for the LIDC-IDRI dataset. Our results show that the mixture models (Mixture FC and Mixture FC-LR) achieve an optimal combination of overlap and diversity to emerge as the best performing models with respect to the GED.

In Figure 3(b), there is no statistically significant difference in the overlap trends between a majority of the models. The results show that samples from the model ensemble have a higher sample diversity compared to the rest of the models, leading to better performance with respect to the GED metric.

In Figure 3 we see different trends for the LIDC-IDRI and WMH datasets. This relates to the fundamental difference between the datasets, in particular, the structures of interest and the variations therein. The difference between the datasets with respect to the inter-rater agreement can be seen in Figure 4. In the example shown, the different raters produce similar segmentations for the WMH dataset, whereas the differences are more noticeable for the LIDC-IDRI example. The inter-rater variability trends can be seen in Figure 3, which show that the WMH dataset has a lower diversity in its labels compared to the LIDC-IDRI datasets. Furthermore, compared to tumors, hyperintensities are smaller structures and therefore any variation present is extremely local. Our results (Figure 2) demonstrate that model ensembles and MC-Dropout are better choices to capture spatially local variation, while Probabilistic U-Net variants are better at capturing more long-range variation and increased rater disagreement.

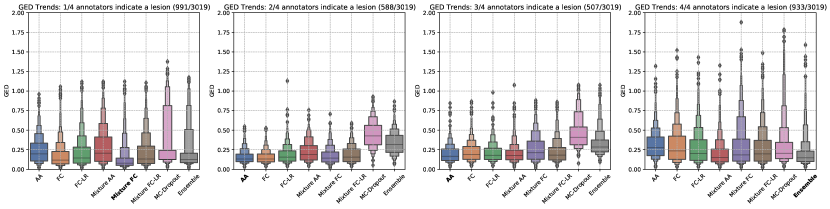
The consequence of the overlap-diversity balance for the LIDC-IDRI dataset can be seen clearly in Figure 5. For segmentations with larger degree of agreement between raters, that is, where one out of four or four out of four raters agree on the presence of a lesion, the MC-Dropout and ensemble models perform on par with the Generalized Probabilistic U-Net configurations with respect to the GED metric. In the other cases, the Generalized Probabilistic U-Net configurations do better since they are able to better estimate uncertainty by also capturing the rarer samples from the label distribution. This is something the MC-Dropout and ensemble were unable to do, leading to a mismatch between the prediction and label distributions. Intuitively, it can be argued that the latent space of the Generalized Probabilistic U-Net seeks to learn the distribution of labels as part of its training objective, thereby enabling them to model the rarer variants and capture rater disagreement. In contrast, MC-Dropout and model ensembles might produce diverse samples either through sub-sampling of model weights (MC-Dropout) or differing optimization trajectories (model ensembles). This diversity might not correspond to the true distribution of the labels because the objective function for these models usually correspond to maximising accuracy.

Figure 6 shows the influence of the rank hyperparameter on the GED trends for both datasets. Our results show that there is no clear relationship between the rank used to construct the covariance matrix and the trends in the GED metric. A similar observation was reported in Monteiro et al. (2020) when the low-rank factor method was used to construct the covariance matrix for the logit (pre-softmax) layer. The results for the LIDC-IDRI dataset show that for all latent space dimensions, there exists an FC-LR configuration that outperforms the FC configuration. The difference between the FC and FC-LR configurations lies in the method used to construct the covariance matrix, which might indicate that the low-rank factor method is a better method. However, the trends for the WMH dataset provide no such indication because there is no statistically significant difference between the FC and best performing FC-LR configurations for the latent space dimensions studied.

Figure 7 shows changes in the GED metric trends as we increase the number of raters used during training. The trends seen for the Generalized Probabilistic U-Net configurations seem to be intuitive for both datasets, that is, using more than one rater during training leads to an improvement in the GED on the test-set. However, the extent of generalization, that is, the decrease in GED, is different for the different variants. For MC-Dropout and the model ensemble, we observed little change in the GED trends as the number of raters was increased. This shows that while these methods do produce predictions with some variation, they do not really capture the inter-rater differences in any meaningful manner.

Our results show that achieving a good match between the prediction and ground truth distributions depends on striking the optimal (with respect to the dataset) balance between overlap and diversity. The structure of interest and variability between raters dictates the choice of the model that achieves that optimal balance. The hyperintensities in the WMH dataset are uniform in structure, with a larger agreement among raters. The Generalized Probabilistic U-Net configurations fail to produce predictions that match the label distribution, with the model ensemble being the best choice. On the other hand, the tumors in the LIDC-IDRI dataset have a more varied structure (between different patients) and more variability in the segmentations (for the same patient) as compared to the WMH dataset. Our results show that MC-Dropout and the model ensemble fail to capture this variability, and the Generalized Probabilistic U-Net configurations are a better choice. Within the Generalized Probabilistic U-Net configurations, we found models that used a mixture of Gaussians to model the latent space distributions performed best.

All Generalized Probabilistic U-Net configurations showed poor performance in the single rater scenario, when only annotations from one rater were used during training. However, the original Probabilistic U-Net framework was not designed for this scenario. Our results confirm that using the (Generalized) Probabilistic U-Net is a suboptimal choice when segmentations from only one rater are available for training.

We treated the number of Gaussians in the mixture model as a hyperparameter that was fixed at the start of training. Future implementations could treat it as a learned parameter, where the final number of Gaussians can be optimized during training. Similar to Kohl et al. (2018) and Baumgartner et al. (2019), we used random sampling to select ground truth segmentations during training. Studying the interplay between different label fusion methods (Warfield et al., 2004; Jensen et al., 2019) and latent space distributions is an interesting research direction. Our extensions to model more general forms of the Gaussian distribution can easily be integrated into a hierarchical latent space model such as PHISeg (Baumgartner et al., 2019). Future research could be directed at studying the efficacy of different latent space distributions at different resolutions in a hierarchical model.

Our results show that the Generalized Probabilistic U-Net is a good choice for segmenting ambiguous medical images, where ambiguity is quantified by disagreement between annotators. Furthermore, choosing more general forms of the Gaussian distribution as the latent space distribution results in statistically significant improvements over the default axis-aligned distribution, as measured by the GED metric on the (more ambiguous) LIDC-IDRI dataset. It is therefore advised to explore alternative Gaussian distributions, since the default choice of axis-aligned Gaussian for the latent space distribution is never the optimal choice in our experiments.

5 Conclusions

Our work focused on extending the Probabilistic U-Net framework by going beyond the axis-aligned Gaussian distribution as the de facto choice for the variational distribution. Our results showed that the choice of model (or latent space distribution) is dictated by the optimal overlap-diversity combination for a particular dataset. Therefore, investigating the suitability of different latent space distributions for a particular dataset is beneficial. The distributions studied in this paper can be used as a drop-in replacement for the axis-aligned Gaussian in other extensions to the Probabilistic U-Net framework, like the class of models using hierarchical latent spaces (Baumgartner et al., 2019), or as base distributions for normalizing flow-based segmentation models (Selvan et al., 2020).

6 Acknowledgements

This work was financially supported by the project IMPACT (Intelligence based iMprovement of Personalized treatment And Clinical workflow supporT) in the framework of the EU research programme ITEA3 (Information Technology for European Advancement).

Ethical Standards

The work follows appropriate ethical standards in conducting research and writing the manuscript, following all applicable laws and regulations regarding treatment of animals or human subjects. The UMCU Medical Ethical Committee has reviewed this study and informed consent was waived due to its retrospective nature.

Conflicts of Interest

The authors declare no conflict of interest.

References

Armato et al. (2011) Samuel G. Armato, Geoffrey McLennan, Luc Bidaut, Michael F. McNitt-Gray, Charles R. Meyer, Anthony P. Reeves, Binsheng Zhao, Denise R. Aberle, et al. The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): A Completed Reference Database of Lung Nodules on CT Scans. Medical Physics, 38(2):915–931, February 2011. ISSN 0094-2405. doi: 10.1118/1.3528204.
Armen Der Kiureghian and Ditlevsen (2009) Armen Der Kiureghian and Ove Ditlevsen. Aleatory or epistemic? Does it matter? Structural Safety, 31(2):105–112, March 2009. ISSN 0167-4730. doi: 10.1016/j.strusafe.2008.06.020.
Barber and Bishop (1997) David Barber and Christopher Bishop. Ensemble learning for multi-layer networks. In M. Jordan, M. Kearns, and S. Solla, editors, Advances in Neural Information Processing Systems, volume 10, pages 395 – 401. MIT Press, 1997. URL https://proceedings.neurips.cc/paper/1997/file/e816c635cad85a60fabd6b97b03cbcc9-Paper.pdf.
Baumgartner et al. (2019) Christian F. Baumgartner, Kerem C. Tezcan, Krishna Chaitanya, Andreas M. Hötker, Urs J. Muehlematter, Khoschy Schawkat, Anton S. Becker, Olivio Donati, and Ender Konukoglu. PHiSeg: Capturing Uncertainty in Medical Image Segmentation. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, Lecture Notes in Computer Science, pages 119–127. Springer International Publishing, 2019. ISBN 978-3-030-32245-8. doi: 10.1007/978-3-030-32245-8˙14.
Bhat et al. (2022) Ishaan Bhat, Josien P. W. Pluim, and Hugo J. Kuijf. Generalized probabilistic u-net for medical image segementation. In Carole H. Sudre, Christian F. Baumgartner, Adrian Dalca, Chen Qin, Ryutaro Tanno, Koen Van Leemput, and William M. Wells III, editors, Uncertainty for Safe Utilization of Machine Learning in Medical Imaging, pages 113–124, Cham, 2022. Springer Nature Switzerland. ISBN 978-3-031-16749-2. doi: 10.1007/978-3-031-16749-2˙11.
Bishop (2006) Christopher M. Bishop. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag, 2006. ISBN:978-0-387-31073-2.
Blundell et al. (2015) Charles Blundell, Julien Cornebise, Koray Kavukcuoglu, and Daan Wierstra. Weight uncertainty in neural network. In Francis Bach and David Blei, editors, Proceedings of the 32nd International Conference on Machine Learning, volume 37, pages 1613–1622. PMLR, 2015. URL https://proceedings.mlr.press/v37/blundell15.html.
Chotzoglou and Kainz (2019) Elisa Chotzoglou and Bernhard Kainz. Exploring the Relationship Between Segmentation Uncertainty, Segmentation Performance and Inter-observer Variability with Probabilistic Networks. In Large-Scale Annotation of Biomedical Data and Expert Label Synthesis and Hardware Aware Learning for Medical Imaging and Computer Assisted Intervention, volume 11851, pages 51–60. Springer International Publishing, 2019. doi: 10.1007/978-3-030-33642-4˙6.
Gal and Ghahramani (2016) Yarin Gal and Zoubin Ghahramani. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Maria Florina Balcan and Kilian Q. Weinberger, editors, Proceedings of The 33rd International Conference on Machine Learning, volume 48 of Proceedings of Machine Learning Research, pages 1050–1059. PMLR, 20–22 Jun 2016. URL https://proceedings.mlr.press/v48/gal16.html.
Hershey and Olsen (2007) John R. Hershey and Peder A. Olsen. Approximating the kullback leibler divergence between gaussian mixture models. In 2007 IEEE International Conference on Acoustics, Speech and Signal Processing - ICASSP ’07, volume 4, pages IV–317–IV–320, 2007. doi: 10.1109/ICASSP.2007.366913.
Higgins et al. (2017) Irina Higgins, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, and Alexander Lerchner. beta-VAE: Learning basic visual concepts with a constrained variational framework. In International Conference on Learning Representations, 2017. URL https://openreview.net/forum?id=Sy2fzU9gl.
Hu et al. (2019) Shi Hu, Daniel Worrall, Stefan Knegt, Bas Veeling, Henkjan Huisman, and Max Welling. Supervised Uncertainty Quantification for Segmentation with Multiple Annotations. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, Lecture Notes in Computer Science, pages 137–145. Springer International Publishing, 2019. ISBN 978-3-030-32245-8. doi: 10.1007/978-3-030-32245-8˙16.
Iglesias et al. (2011) Juan Eugenio Iglesias, Cheng-Yi Liu, Paul M. Thompson, and Zhuowen Tu. Robust brain extraction across datasets and comparison with publicly available methods. IEEE Transactions on Medical Imaging, 30(9):1617–1634, 2011. doi: 10.1109/TMI.2011.2138152.
Ioffe and Szegedy (2015) Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Francis Bach and David Blei, editors, Proceedings of the 32nd International Conference on Machine Learning, volume 37 of Proceedings of Machine Learning Research, pages 448–456. PMLR, 2015. URL https://proceedings.mlr.press/v37/ioffe15.html.
Jang et al. (2017) Eric Jang, Shixiang Gu, and Ben Poole. Categorical reparameterization with gumbel-softmax. In International Conference on Learning Representations, 2017. URL https://openreview.net/forum?id=rkE3y85ee.
Jensen et al. (2019) Martin Holm Jensen, Dan Richter Jørgensen, Raluca Jalaboi, Mads Eiler Hansen, and Martin Aastrup Olsen. Improving Uncertainty Estimation in Convolutional Neural Networks Using Inter-rater Agreement. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, volume 11767, pages 540–548. Springer International Publishing, 2019. doi: 10.1007/978-3-030-32251-9˙59.
Jiang et al. (2017) Zhuxi Jiang, Yin Zheng, Huachun Tan, Bangsheng Tang, and Hanning Zhou. Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, pages 1965–1972. International Joint Conferences on Artificial Intelligence Organization, August 2017. ISBN 978-0-9992411-0-3. doi: 10.24963/ijcai.2017/273.
Jungo et al. (2018) Alain Jungo, Raphael Meier, Ekin Ermis, Marcela Blatti-Moreno, Evelyn Herrmann, Roland Wiest, and Mauricio Reyes. On the Effect of Inter-observer Variability for a Reliable Estimation of Uncertainty of Medical Image Segmentation. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2018, pages 682–690. Springer International Publishing, 2018. doi: 10.1007/978-3-030-00928-1˙77.
Jungo et al. (2020) Alain Jungo, Fabian Balsiger, and Mauricio Reyes. Analyzing the Quality and Challenges of Uncertainty Estimations for Brain Tumor Segmentation. Frontiers in Neuroscience, 14, April 2020. ISSN 1662-453X. doi: 10.3389/fnins.2020.00282.
Kamnitsas et al. (2018) K. Kamnitsas, W. Bai, E. Ferrante, S. McDonagh, M. Sinclair, N. Pawlowski, M. Rajchl, M. Lee, B. Kainz, D. Rueckert, and B. Glocker. Ensembles of multiple models and architectures for robust brain tumour segmentation. In Alessandro Crimi, Spyridon Bakas, Hugo Kuijf, Bjoern Menze, and Mauricio Reyes, editors, Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, pages 450–462, Cham, 2018. Springer International Publishing. ISBN 978-3-319-75238-9. doi: 10.1007/978-3-319-75238-9˙38.
Kendall and Gal (2017) Alex Kendall and Yarin Gal. What uncertainties do we need in bayesian deep learning for computer vision? In I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017. URL https://proceedings.neurips.cc/paper/2017/file/2650d6089a6d640c5e85b2b88265dc2b-Paper.pdf.
Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. Adam: A Method for Stochastic Optimization. In International Conference on Learning Representations, 2015. URL https://hdl.handle.net/11245/1.505367.
Kingma and Welling (2014) Diederik P. Kingma and Max Welling. Auto-Encoding Variational Bayes. In International Conference on Learning Representations, 2014. URL https://hdl.handle.net/11245/1.434281.
Kingma and Welling (2019) Diederik P. Kingma and Max Welling. An Introduction to Variational Autoencoders. Foundations and Trends® in Machine Learning, 12(4):307–392, 2019. ISSN 1935-8237, 1935-8245. doi: 10.1561/2200000056.
Kingma et al. (2015) Durk P Kingma, Tim Salimans, and Max Welling. Variational Dropout and the Local Reparameterization Trick. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015. URL https://proceedings.neurips.cc/paper/2015/hash/bc7316929fe1545bf0b98d114ee3ecb8-Abstract.html.
Klein et al. (2010) S. Klein, M. Staring, K. Murphy, M.A. Viergever, and J.P.W. Pluim. Elastix : a toolbox for intensity-based medical image registration. IEEE Transactions on Medical Imaging, 29(1):196–205, 2010. ISSN 0278-0062. doi: 10.1109/TMI.2009.2035616.
Kohl et al. (2018) Simon Kohl, Bernardino Romera-Paredes, Clemens Meyer, Jeffrey De Fauw, Joseph R. Ledsam, Klaus Maier-Hein, S. M. Ali Eslami, Danilo Jimenez Rezende, and Olaf Ronneberger. A Probabilistic U-Net for Segmentation of Ambiguous Images. In Advances in Neural Information Processing Systems, volume 31. Curran Associates, Inc., 2018. URL https://papers.nips.cc/paper/2018/hash/473447ac58e1cd7e96172575f48dca3b-Abstract.html.
Kopf et al. (2021) Andreas Kopf, Vincent Fortuin, Vignesh Ram Somnath, and Manfred Claassen. Mixture-of-Experts Variational Autoencoder for clustering and generating from similarity-based representations on single cell data. PLOS Computational Biology, 17(6):e1009086, June 2021. ISSN 1553-7358. doi: 10.1371/journal.pcbi.1009086.
Kuijf et al. (2019) Hugo J. Kuijf, J. Matthijs Biesbroek, Jeroen De Bresser, Rutger Heinen, Simon Andermatt, Mariana Bento, Matt Berseth, Mikhail Belyaev, M. Jorge Cardoso, Adrià Casamitjana, D. Louis Collins, Mahsa Dadar, Achilleas Georgiou, Mohsen Ghafoorian, Dakai Jin, April Khademi, Jesse Knight, Hongwei Li, Xavier Lladó, Miguel Luna, Qaiser Mahmood, Richard McKinley, Alireza Mehrtash, Sébastien Ourselin, Bo-Yong Park, Hyunjin Park, Sang Hyun Park, Simon Pezold, Elodie Puybareau, Leticia Rittner, Carole H. Sudre, Sergi Valverde, Verónica Vilaplana, Roland Wiest, Yongchao Xu, Ziyue Xu, Guodong Zeng, Jianguo Zhang, Guoyan Zheng, Christopher Chen, Wiesje van der Flier, Frederik Barkhof, Max A. Viergever, and Geert Jan Biessels. Standardized assessment of automatic segmentation of white matter hyperintensities and results of the wmh segmentation challenge. IEEE Transactions on Medical Imaging, 38(11):2556–2568, 2019. doi: 10.1109/TMI.2019.2905770.
Lakshminarayanan et al. (2017) Balaji Lakshminarayanan, Alexander Pritzel, and Charles Blundell. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. In Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017. URL https://proceedings.neurips.cc/paper/2017/file/9ef2ed4b7fd2c810847ffa5fa85bce38-Paper.pdf.
Maddison et al. (2017) Chris J. Maddison, Andriy Mnih, and Yee Whye Teh. The concrete distribution: A continuous relaxation of discrete random variables. In International Conference on Learning Representations, 2017. URL https://openreview.net/forum?id=S1jE5L5gl.
Mehrtash et al. (2020) Alireza Mehrtash, William M. Wells, Clare M. Tempany, Purang Abolmaesumi, and Tina Kapur. Confidence calibration and predictive uncertainty estimation for deep medical image segmentation. IEEE Transactions on Medical Imaging, 39(12):3868–3878, 2020. doi: 10.1109/TMI.2020.3006437.
Monteiro et al. (2020) Miguel Monteiro, Loic Le Folgoc, Daniel Coelho de Castro, Nick Pawlowski, Bernardo Marques, Konstantinos Kamnitsas, Mark van der Wilk, and Ben Glocker. Stochastic segmentation networks: Modelling spatially correlated aleatoric uncertainty. In H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, and H. Lin, editors, Advances in Neural Information Processing Systems, volume 33, pages 12756–12767. Curran Associates, Inc., 2020. URL https://proceedings.neurips.cc/paper/2020/file/95f8d9901ca8878e291552f001f67692-Paper.pdf.
Paszke et al. (2019) Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, high-performance deep learning library. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems 32, pages 8024–8035. Curran Associates, Inc., 2019. URL https://papers.nips.cc/paper/2019/hash/bdbca288fee7f92f2bfa9f7012727740-Abstract.html.
Rezende and Mohamed (2015) Danilo Rezende and Shakir Mohamed. Variational inference with normalizing flows. In Francis Bach and David Blei, editors, Proceedings of the 32nd International Conference on Machine Learning, volume 37 of Proceedings of Machine Learning Research, pages 1530–1538. PMLR, 2015. URL https://proceedings.mlr.press/v37/rezende15.html.
Rezende et al. (2014) Danilo Jimenez Rezende, Shakir Mohamed, and Daan Wierstra. Stochastic backpropagation and approximate inference in deep generative models. In Eric P. Xing and Tony Jebara, editors, Proceedings of the 31st International Conference on Machine Learning, volume 32 of Proceedings of Machine Learning Research, pages 1278–1286. PMLR, 2014. URL https://proceedings.mlr.press/v32/rezende14.html.
Ronneberger et al. (2015) Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, pages 234–241. Springer International Publishing, 2015. ISBN 978-3-319-24574-4. doi: 10.1007/978-3-319-24574-4˙28.
Rupprecht et al. (2017) Christian Rupprecht, Iro Laina, Robert DiPietro, Maximilian Baust, Federico Tombari, Nassir Navab, and Gregory D. Hager. Learning in an Uncertain World: Representing Ambiguity Through Multiple Hypotheses. In 2017 IEEE International Conference on Computer Vision (ICCV), pages 3611–3620, October 2017. doi: 10.1109/ICCV.2017.388.
Selvan et al. (2020) Raghavendra Selvan, Frederik Faye, Jon Middleton, and Akshay Pai. Uncertainty quantification in medical image segmentation with normalizing flows. In Mingxia Liu, Pingkun Yan, Chunfeng Lian, and Xiaohuan Cao, editors, Machine Learning in Medical Imaging, pages 80–90, Cham, 2020. Springer International Publishing. ISBN 978-3-030-59861-7. doi: 10.1007/978-3-030-59861-7˙9.
Sohn et al. (2015) Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning Structured Output Representation using Deep Conditional Generative Models. In Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015. URL https://proceedings.neurips.cc/paper/2015/file/8d55a249e6baa5c06772297520da2051-Paper.pdf.
Srivastava et al. (2014) Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15(56):1929–1958, 2014. URL http://jmlr.org/papers/v15/srivastava14a.html.
Teye et al. (2018) Mattias Teye, Hossein Azizpour, and Kevin Smith. Bayesian uncertainty estimation for batch normalized deep networks. In Jennifer Dy and Andreas Krause, editors, Proceedings of the 35th International Conference on Machine Learning, volume 80 of Proceedings of Machine Learning Research, pages 4907–4916. PMLR, 2018. URL https://proceedings.mlr.press/v80/teye18a.html.
Wainwright and Jordan (2007) Martin J. Wainwright and Michael I. Jordan. Graphical Models, Exponential Families, and Variational Inference. Foundations and Trends® in Machine Learning, 1(1–2):1–305, 2007. ISSN 1935-8237, 1935-8245. doi: 10.1561/2200000001.
Wang et al. (2019) Guotai Wang, Wenqi Li, Michael Aertsen, Jan Deprest, Sébastien Ourselin, and Tom Vercauteren. Aleatoric uncertainty estimation with test-time augmentation for medical image segmentation with convolutional neural networks. Neurocomputing, 338:34 – 45, 2019. ISSN 0925-2312. doi: https://doi.org/10.1016/j.neucom.2019.01.103.
Warfield et al. (2004) S.K. Warfield, K.H. Zou, and W.M. Wells. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Transactions on Medical Imaging, 23(7):903–921, July 2004. ISSN 1558-254X. doi: 10.1109/TMI.2004.828354.
Williams (1996) Peter M. Williams. Using neural networks to model conditional multivariate densities. Neural Comput., 8(4):843–854, may 1996. ISSN 0899-7667. doi: 10.1162/neco.1996.8.4.843.

[bib.bib1] Armato et al. (2011) Samuel G. Armato, Geoffrey McLennan, Luc Bidaut, Michael F. McNitt-Gray, Charles R. Meyer, Anthony P. Reeves, Binsheng Zhao, Denise R. Aberle, et al. The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): A Completed Reference Database of Lung Nodules on CT Scans. Medical Physics, 38(2):915–931, February 2011. ISSN 0094-2405. doi: 10.1118/1.3528204.

[bib.bib2] Armen Der Kiureghian and Ditlevsen (2009) Armen Der Kiureghian and Ove Ditlevsen. Aleatory or epistemic? Does it matter? Structural Safety, 31(2):105–112, March 2009. ISSN 0167-4730. doi: 10.1016/j.strusafe.2008.06.020.

[bib.bib3] Barber and Bishop (1997) David Barber and Christopher Bishop. Ensemble learning for multi-layer networks. In M. Jordan, M. Kearns, and S. Solla, editors, Advances in Neural Information Processing Systems, volume 10, pages 395 – 401. MIT Press, 1997. URL https://proceedings.neurips.cc/paper/1997/file/e816c635cad85a60fabd6b97b03cbcc9-Paper.pdf.

[bib.bib4] Baumgartner et al. (2019) Christian F. Baumgartner, Kerem C. Tezcan, Krishna Chaitanya, Andreas M. Hötker, Urs J. Muehlematter, Khoschy Schawkat, Anton S. Becker, Olivio Donati, and Ender Konukoglu. PHiSeg: Capturing Uncertainty in Medical Image Segmentation. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, Lecture Notes in Computer Science, pages 119–127. Springer International Publishing, 2019. ISBN 978-3-030-32245-8. doi: 10.1007/978-3-030-32245-8˙14.

[bib.bib5] Bhat et al. (2022) Ishaan Bhat, Josien P. W. Pluim, and Hugo J. Kuijf. Generalized probabilistic u-net for medical image segementation. In Carole H. Sudre, Christian F. Baumgartner, Adrian Dalca, Chen Qin, Ryutaro Tanno, Koen Van Leemput, and William M. Wells III, editors, Uncertainty for Safe Utilization of Machine Learning in Medical Imaging, pages 113–124, Cham, 2022. Springer Nature Switzerland. ISBN 978-3-031-16749-2. doi: 10.1007/978-3-031-16749-2˙11.

[bib.bib6] Bishop (2006) Christopher M. Bishop. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag, 2006. ISBN:978-0-387-31073-2.

[bib.bib7] Blundell et al. (2015) Charles Blundell, Julien Cornebise, Koray Kavukcuoglu, and Daan Wierstra. Weight uncertainty in neural network. In Francis Bach and David Blei, editors, Proceedings of the 32nd International Conference on Machine Learning, volume 37, pages 1613–1622. PMLR, 2015. URL https://proceedings.mlr.press/v37/blundell15.html.

[bib.bib8] Chotzoglou and Kainz (2019) Elisa Chotzoglou and Bernhard Kainz. Exploring the Relationship Between Segmentation Uncertainty, Segmentation Performance and Inter-observer Variability with Probabilistic Networks. In Large-Scale Annotation of Biomedical Data and Expert Label Synthesis and Hardware Aware Learning for Medical Imaging and Computer Assisted Intervention, volume 11851, pages 51–60. Springer International Publishing, 2019. doi: 10.1007/978-3-030-33642-4˙6.

[bib.bib9] Gal and Ghahramani (2016) Yarin Gal and Zoubin Ghahramani. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Maria Florina Balcan and Kilian Q. Weinberger, editors, Proceedings of The 33rd International Conference on Machine Learning, volume 48 of Proceedings of Machine Learning Research, pages 1050–1059. PMLR, 20–22 Jun 2016. URL https://proceedings.mlr.press/v48/gal16.html.

[bib.bib10] Hershey and Olsen (2007) John R. Hershey and Peder A. Olsen. Approximating the kullback leibler divergence between gaussian mixture models. In 2007 IEEE International Conference on Acoustics, Speech and Signal Processing - ICASSP ’07, volume 4, pages IV–317–IV–320, 2007. doi: 10.1109/ICASSP.2007.366913.

[bib.bib11] Higgins et al. (2017) Irina Higgins, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, and Alexander Lerchner. beta-VAE: Learning basic visual concepts with a constrained variational framework. In International Conference on Learning Representations, 2017. URL https://openreview.net/forum?id=Sy2fzU9gl.

[bib.bib12] Hu et al. (2019) Shi Hu, Daniel Worrall, Stefan Knegt, Bas Veeling, Henkjan Huisman, and Max Welling. Supervised Uncertainty Quantification for Segmentation with Multiple Annotations. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, Lecture Notes in Computer Science, pages 137–145. Springer International Publishing, 2019. ISBN 978-3-030-32245-8. doi: 10.1007/978-3-030-32245-8˙16.

[bib.bib13] Iglesias et al. (2011) Juan Eugenio Iglesias, Cheng-Yi Liu, Paul M. Thompson, and Zhuowen Tu. Robust brain extraction across datasets and comparison with publicly available methods. IEEE Transactions on Medical Imaging, 30(9):1617–1634, 2011. doi: 10.1109/TMI.2011.2138152.

[bib.bib14] Ioffe and Szegedy (2015) Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Francis Bach and David Blei, editors, Proceedings of the 32nd International Conference on Machine Learning, volume 37 of Proceedings of Machine Learning Research, pages 448–456. PMLR, 2015. URL https://proceedings.mlr.press/v37/ioffe15.html.

[bib.bib15] Jang et al. (2017) Eric Jang, Shixiang Gu, and Ben Poole. Categorical reparameterization with gumbel-softmax. In International Conference on Learning Representations, 2017. URL https://openreview.net/forum?id=rkE3y85ee.

[bib.bib16] Jensen et al. (2019) Martin Holm Jensen, Dan Richter Jørgensen, Raluca Jalaboi, Mads Eiler Hansen, and Martin Aastrup Olsen. Improving Uncertainty Estimation in Convolutional Neural Networks Using Inter-rater Agreement. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, volume 11767, pages 540–548. Springer International Publishing, 2019. doi: 10.1007/978-3-030-32251-9˙59.

[bib.bib17] Jiang et al. (2017) Zhuxi Jiang, Yin Zheng, Huachun Tan, Bangsheng Tang, and Hanning Zhou. Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, pages 1965–1972. International Joint Conferences on Artificial Intelligence Organization, August 2017. ISBN 978-0-9992411-0-3. doi: 10.24963/ijcai.2017/273.

[bib.bib18] Jungo et al. (2018) Alain Jungo, Raphael Meier, Ekin Ermis, Marcela Blatti-Moreno, Evelyn Herrmann, Roland Wiest, and Mauricio Reyes. On the Effect of Inter-observer Variability for a Reliable Estimation of Uncertainty of Medical Image Segmentation. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2018, pages 682–690. Springer International Publishing, 2018. doi: 10.1007/978-3-030-00928-1˙77.

[bib.bib19] Jungo et al. (2020) Alain Jungo, Fabian Balsiger, and Mauricio Reyes. Analyzing the Quality and Challenges of Uncertainty Estimations for Brain Tumor Segmentation. Frontiers in Neuroscience, 14, April 2020. ISSN 1662-453X. doi: 10.3389/fnins.2020.00282.

[bib.bib20] Kamnitsas et al. (2018) K. Kamnitsas, W. Bai, E. Ferrante, S. McDonagh, M. Sinclair, N. Pawlowski, M. Rajchl, M. Lee, B. Kainz, D. Rueckert, and B. Glocker. Ensembles of multiple models and architectures for robust brain tumour segmentation. In Alessandro Crimi, Spyridon Bakas, Hugo Kuijf, Bjoern Menze, and Mauricio Reyes, editors, Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, pages 450–462, Cham, 2018. Springer International Publishing. ISBN 978-3-319-75238-9. doi: 10.1007/978-3-319-75238-9˙38.

[bib.bib21] Kendall and Gal (2017) Alex Kendall and Yarin Gal. What uncertainties do we need in bayesian deep learning for computer vision? In I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017. URL https://proceedings.neurips.cc/paper/2017/file/2650d6089a6d640c5e85b2b88265dc2b-Paper.pdf.

[bib.bib22] Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. Adam: A Method for Stochastic Optimization. In International Conference on Learning Representations, 2015. URL https://hdl.handle.net/11245/1.505367.

[bib.bib23] Kingma and Welling (2014) Diederik P. Kingma and Max Welling. Auto-Encoding Variational Bayes. In International Conference on Learning Representations, 2014. URL https://hdl.handle.net/11245/1.434281.

[bib.bib24] Kingma and Welling (2019) Diederik P. Kingma and Max Welling. An Introduction to Variational Autoencoders. Foundations and Trends® in Machine Learning, 12(4):307–392, 2019. ISSN 1935-8237, 1935-8245. doi: 10.1561/2200000056.

[bib.bib25] Kingma et al. (2015) Durk P Kingma, Tim Salimans, and Max Welling. Variational Dropout and the Local Reparameterization Trick. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015. URL https://proceedings.neurips.cc/paper/2015/hash/bc7316929fe1545bf0b98d114ee3ecb8-Abstract.html.

[bib.bib26] Klein et al. (2010) S. Klein, M. Staring, K. Murphy, M.A. Viergever, and J.P.W. Pluim. Elastix : a toolbox for intensity-based medical image registration. IEEE Transactions on Medical Imaging, 29(1):196–205, 2010. ISSN 0278-0062. doi: 10.1109/TMI.2009.2035616.

[bib.bib27] Kohl et al. (2018) Simon Kohl, Bernardino Romera-Paredes, Clemens Meyer, Jeffrey De Fauw, Joseph R. Ledsam, Klaus Maier-Hein, S. M. Ali Eslami, Danilo Jimenez Rezende, and Olaf Ronneberger. A Probabilistic U-Net for Segmentation of Ambiguous Images. In Advances in Neural Information Processing Systems, volume 31. Curran Associates, Inc., 2018. URL https://papers.nips.cc/paper/2018/hash/473447ac58e1cd7e96172575f48dca3b-Abstract.html.

[bib.bib28] Kopf et al. (2021) Andreas Kopf, Vincent Fortuin, Vignesh Ram Somnath, and Manfred Claassen. Mixture-of-Experts Variational Autoencoder for clustering and generating from similarity-based representations on single cell data. PLOS Computational Biology, 17(6):e1009086, June 2021. ISSN 1553-7358. doi: 10.1371/journal.pcbi.1009086.

[bib.bib29] Kuijf et al. (2019) Hugo J. Kuijf, J. Matthijs Biesbroek, Jeroen De Bresser, Rutger Heinen, Simon Andermatt, Mariana Bento, Matt Berseth, Mikhail Belyaev, M. Jorge Cardoso, Adrià Casamitjana, D. Louis Collins, Mahsa Dadar, Achilleas Georgiou, Mohsen Ghafoorian, Dakai Jin, April Khademi, Jesse Knight, Hongwei Li, Xavier Lladó, Miguel Luna, Qaiser Mahmood, Richard McKinley, Alireza Mehrtash, Sébastien Ourselin, Bo-Yong Park, Hyunjin Park, Sang Hyun Park, Simon Pezold, Elodie Puybareau, Leticia Rittner, Carole H. Sudre, Sergi Valverde, Verónica Vilaplana, Roland Wiest, Yongchao Xu, Ziyue Xu, Guodong Zeng, Jianguo Zhang, Guoyan Zheng, Christopher Chen, Wiesje van der Flier, Frederik Barkhof, Max A. Viergever, and Geert Jan Biessels. Standardized assessment of automatic segmentation of white matter hyperintensities and results of the wmh segmentation challenge. IEEE Transactions on Medical Imaging, 38(11):2556–2568, 2019. doi: 10.1109/TMI.2019.2905770.

[bib.bib30] Lakshminarayanan et al. (2017) Balaji Lakshminarayanan, Alexander Pritzel, and Charles Blundell. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. In Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017. URL https://proceedings.neurips.cc/paper/2017/file/9ef2ed4b7fd2c810847ffa5fa85bce38-Paper.pdf.

[bib.bib31] Maddison et al. (2017) Chris J. Maddison, Andriy Mnih, and Yee Whye Teh. The concrete distribution: A continuous relaxation of discrete random variables. In International Conference on Learning Representations, 2017. URL https://openreview.net/forum?id=S1jE5L5gl.

[bib.bib32] Mehrtash et al. (2020) Alireza Mehrtash, William M. Wells, Clare M. Tempany, Purang Abolmaesumi, and Tina Kapur. Confidence calibration and predictive uncertainty estimation for deep medical image segmentation. IEEE Transactions on Medical Imaging, 39(12):3868–3878, 2020. doi: 10.1109/TMI.2020.3006437.

[bib.bib33] Monteiro et al. (2020) Miguel Monteiro, Loic Le Folgoc, Daniel Coelho de Castro, Nick Pawlowski, Bernardo Marques, Konstantinos Kamnitsas, Mark van der Wilk, and Ben Glocker. Stochastic segmentation networks: Modelling spatially correlated aleatoric uncertainty. In H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, and H. Lin, editors, Advances in Neural Information Processing Systems, volume 33, pages 12756–12767. Curran Associates, Inc., 2020. URL https://proceedings.neurips.cc/paper/2020/file/95f8d9901ca8878e291552f001f67692-Paper.pdf.

[bib.bib34] Paszke et al. (2019) Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, high-performance deep learning library. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems 32, pages 8024–8035. Curran Associates, Inc., 2019. URL https://papers.nips.cc/paper/2019/hash/bdbca288fee7f92f2bfa9f7012727740-Abstract.html.

[bib.bib35] Rezende and Mohamed (2015) Danilo Rezende and Shakir Mohamed. Variational inference with normalizing flows. In Francis Bach and David Blei, editors, Proceedings of the 32nd International Conference on Machine Learning, volume 37 of Proceedings of Machine Learning Research, pages 1530–1538. PMLR, 2015. URL https://proceedings.mlr.press/v37/rezende15.html.

[bib.bib36] Rezende et al. (2014) Danilo Jimenez Rezende, Shakir Mohamed, and Daan Wierstra. Stochastic backpropagation and approximate inference in deep generative models. In Eric P. Xing and Tony Jebara, editors, Proceedings of the 31st International Conference on Machine Learning, volume 32 of Proceedings of Machine Learning Research, pages 1278–1286. PMLR, 2014. URL https://proceedings.mlr.press/v32/rezende14.html.

[bib.bib37] Ronneberger et al. (2015) Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, pages 234–241. Springer International Publishing, 2015. ISBN 978-3-319-24574-4. doi: 10.1007/978-3-319-24574-4˙28.

[bib.bib38] Rupprecht et al. (2017) Christian Rupprecht, Iro Laina, Robert DiPietro, Maximilian Baust, Federico Tombari, Nassir Navab, and Gregory D. Hager. Learning in an Uncertain World: Representing Ambiguity Through Multiple Hypotheses. In 2017 IEEE International Conference on Computer Vision (ICCV), pages 3611–3620, October 2017. doi: 10.1109/ICCV.2017.388.

[bib.bib39] Selvan et al. (2020) Raghavendra Selvan, Frederik Faye, Jon Middleton, and Akshay Pai. Uncertainty quantification in medical image segmentation with normalizing flows. In Mingxia Liu, Pingkun Yan, Chunfeng Lian, and Xiaohuan Cao, editors, Machine Learning in Medical Imaging, pages 80–90, Cham, 2020. Springer International Publishing. ISBN 978-3-030-59861-7. doi: 10.1007/978-3-030-59861-7˙9.

[bib.bib40] Sohn et al. (2015) Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning Structured Output Representation using Deep Conditional Generative Models. In Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015. URL https://proceedings.neurips.cc/paper/2015/file/8d55a249e6baa5c06772297520da2051-Paper.pdf.

[bib.bib41] Srivastava et al. (2014) Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15(56):1929–1958, 2014. URL http://jmlr.org/papers/v15/srivastava14a.html.

[bib.bib42] Teye et al. (2018) Mattias Teye, Hossein Azizpour, and Kevin Smith. Bayesian uncertainty estimation for batch normalized deep networks. In Jennifer Dy and Andreas Krause, editors, Proceedings of the 35th International Conference on Machine Learning, volume 80 of Proceedings of Machine Learning Research, pages 4907–4916. PMLR, 2018. URL https://proceedings.mlr.press/v80/teye18a.html.

[bib.bib43] Wainwright and Jordan (2007) Martin J. Wainwright and Michael I. Jordan. Graphical Models, Exponential Families, and Variational Inference. Foundations and Trends® in Machine Learning, 1(1–2):1–305, 2007. ISSN 1935-8237, 1935-8245. doi: 10.1561/2200000001.

[bib.bib44] Wang et al. (2019) Guotai Wang, Wenqi Li, Michael Aertsen, Jan Deprest, Sébastien Ourselin, and Tom Vercauteren. Aleatoric uncertainty estimation with test-time augmentation for medical image segmentation with convolutional neural networks. Neurocomputing, 338:34 – 45, 2019. ISSN 0925-2312. doi: https://doi.org/10.1016/j.neucom.2019.01.103.

[bib.bib45] Warfield et al. (2004) S.K. Warfield, K.H. Zou, and W.M. Wells. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Transactions on Medical Imaging, 23(7):903–921, July 2004. ISSN 1558-254X. doi: 10.1109/TMI.2004.828354.

[bib.bib46] Williams (1996) Peter M. Williams. Using neural networks to model conditional multivariate densities. Neural Comput., 8(4):843–854, may 1996. ISSN 0899-7667. doi: 10.1162/neco.1996.8.4.843.

Effect of latent space distribution on the segmentation of images with multiple annotations

Ishaan Bhat¹, Josien P.W. Pluim², Max A. Viergever¹, Hugo J. Kuijf¹

1: Image Sciences Institute, University Medical Center Utrecht, The Netherlands, 2: Department of Biomedical Engineering, Eindhoven University of Technology, The Netherlands

Publication date: 2023/04/30

https://doi.org/10.59275/j.melba.2023-18ae

Abstract

1 Introduction