1 Introduction
In recent years, deep convolutional neural networks (CNN) have become the standard in different learning problems in computer vision, like classification, localization, and segmentation. Inspired by this development, researchers have proposed CNN architectures for the processing of medical images, in different modalities. Image segmentation is a common task addressed by both the computer vision and the medical image processing communities. Segmentation of medical structures is an initial step in many computer-aided procedures, like computer-assisted navigation and detection. However, the necessity of experts for training-example annotation, the similarity in tissues, and the inter-patient variation of anatomical structures add additional challenges compared with real-world images, leading to potential errors in the CNN predictions.
Organ segmentation in CT has been a topic of research. Recent CNN architectures employ single or multiple aggregations of CNN models, using two-dimensional (Zhou et al., 2017a) or three-dimensional networks (Zhu et al., 2018; Roth et al., 2018). Works that include shape and geometric priors have also been proposed (Zhou et al., 2019; Yao et al., 2019; Degel et al., 2018). A common practice to improve the segmentation of a model is the inclusion of a post-processing refinement step, included after the inference process of the CNN. Methods based on conditional random fields (CRF) (Krähenbühl and Koltun, 2011) are examples of a refinement strategy. Even though refinement methods can be the final step of the segmentation process, it can also serve as an intermediate step for improving model performance. For example, Wang et al. (2018) use a CRF-based method to generate a set of scribbles. In combination with user-defined scribbles, the results are used to perform an image specific fine-tune of a CNN. Similarly, semi-supervised learning methods can use refined predictions as pseudo-labels to allow including unlabeled data in CNN’s training process (Bai et al., 2017). The work in (Li and Ping, 2018) addresses the problem of loss in spatial correlation in the task of metastasis detection in Whole-slide images, due to the subdivision of the image in independent patches. The authors propose an architecture composed of a CNN that processes a group of input patches with a CRF on top. This CRF is employed to consider neighborhood information in the classification task, bringing consistency in the model’s prediction.
CRF employs CNN prediction together with spatial and intensity similarity between the pixels in CT slices to refine the segmentation. In this sense, additional information regarding the correctness of the prediction could bring useful information to the process. Related to this idea, Gal (Kendall and Gal, 2017) shows that a stochastic Gaussian process can be approximated through the dropout layers of regular CNNs, in a process known as Monte Carlo dropout (MCDO). This brings the possibility to estimate the uncertainty of recent CNN segmentation models. CNN uncertainty has proved to be useful as an attention mechanism in semi-supervised learning (Xia et al., 2018). Recent works in computer vision have started to explore its capabilities for finding potential misclassified regions for segmentation refinement purposes (Dias and Medeiros, 2019). In the medical context, the ability of uncertainty to reflect incorrect predictions has been recently studied (Nair et al., 2018). Similarly, a recent work presented by Yu et al. (2019), uses the uncertainty of a teacher model to select the pseudo-labels to train a student model.
Since uncertainty can bring insights regarding the potential errors in the segmentation, we still need a way to incorporate this knowledge into a refinement pipeline. In this work, we propose a method to formulate the segmentation refinement problem of CT data as a semi-supervised graph learning problem, that is solved using graph convolutional neural networks (GCN). Graph representations of three-dimensional data have been applied for refinement (Kamnitsas et al., 2017), similarly, recent works have started to explore the application of graph convolutional networks (GCN) for the segmentation of tubular structures, like airways (Selvan et al., 2018; Juarez et al., 2019) and vessels (Shin et al., 2019). In this work, we explore the use of recent GCNs with sparse graphs-representations of 3-D data for the organ segmentation refinement task.
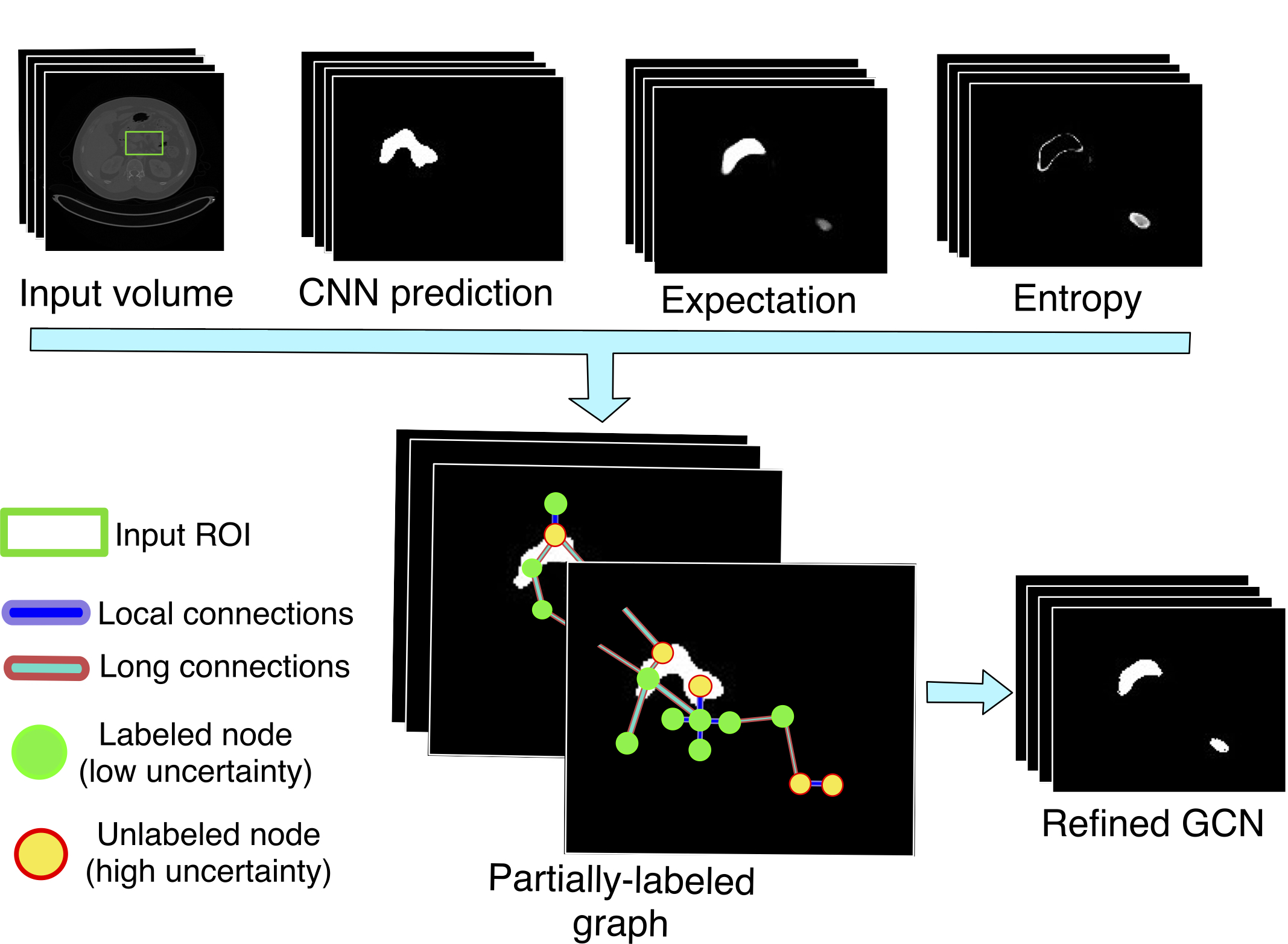
For a given CNN, we first apply MCDO to obtain the model’s expectation and uncertainty, this last expressed by the model’s entropy. This is used to divide the CNN output into high confidence points (background or foreground) and low confidence points. With this information, we define a semi-labeled graph that is used to train a GCN in a semi-supervised way using the high confidence predictions. The refined segmentation is obtained by re-evaluating the full graph in the trained GCN (see Fig. 1). To our best knowledge, this is the first time a semi-supervised GCN learning strategy is employed in the medical image segmentation task, specifically, for single organ segmentation. Also, this work presents one of the first cases of using GCN and uncertainty analysis for organ segmentation refinement. We perform experiments for refining the segmentation of a U-Net on CT data for the pancreas and spleen segmentation problems. We compare our results with the popular CRF refinement method showing a better improvement over the initial CNN prediction and CRF refinement.
This work presents an extension of our initial results presented in Soberanis-Mukul et al. (2020). We have extend our initial analysis into a sensitivity analysis presented in section 3.4. We compare with an additional connectivity scheme in section 3.4.3. We also perform a thorough study on the components of our edge weighting function in sections 3.4.4 to 3.4.8. Finally, we evaluate the performance of the refinement strategy on a second CNN architecture, namely QuickNat (Roy et al., 2019b, a), in section 3.7, and discuss some insights on 2D vs. 3D CNN architectures in section 3.8.
2 Methods
Overview: Consider an input CT volume with the intensity value at the voxel position ; consider also, a trained CNN with parameters ; and a segmented volume with . Our objective, is to refine the segmentation using a GCN trained on a graph representation of the input data. Our framework operates as a post-processing step (one volume at a time) and assumes that no information about the real segmentation (ground truth) is available.
We first look for a binary volume used to highlight the potential false positives and false negatives elements of . The second step uses , together with information coming from , , and , to refine the segmentation . We use uncertainty analysis to define . For the second step, we solve the refinement problem using a semi-supervised GCN trained on a graph representation of our input volume.
2.1 Uncertainty Analysis: Finding Incorrect Elements
Incorrect elements are estimated considering the uncertainty of . We employ MCDO approximation (Kendall and Gal, 2017; Gal and Ghahramani, 2016) to evaluate the uncertainty of the CNN. This strategy can be applied to any model trained with dropout layers, without modifying or retraining the model. This attribute makes it ideal for a post-processing refinement algorithm. Gal and Ghahramani (2016) showed that a neural network trained with dropout layers before the convolutional layers is equivalent to approximate the probabilistic deep Gaussian Process. Following MCDO, we use the dropout layers of the network in inference time, and perform stochastic passes on the network to get the expectation of the model’s prediction:
| (1) |
with the model parameters after applying dropout in the pass . The model uncertainty is given by the entropy, computed as
| (2) |
with being the true probability of the voxel to belong to class , and is the number of classes ( in our binary segmentation scenario). To approximate this probability, we use the expectation of the model’s prediction . Finally, we define the potential incorrect elements by applying a binary threshold on the entropy volume:
| (3) |
where the uncertainty threshold controls the entropy necessary to consider a voxel as uncertain.
2.2 Graph Learning for Segmentation Refinement
At this point, we have a binary mask indicating voxels with high uncertainty. The uncertainty analysis only tells us that the model is not confident about its predictions. Some of the elements indicated by could be indeed correct and its value should not be changed. However, we can use a learning model that trains on high confidence voxels to reclassify (refine) the output of the CNN . Using the information from the uncertainty analysis, we can define a partially-labeled graph, where the voxels are mapped to nodes, and neighborhood relationship to edges. In this way, we formulate the refinement problem as a semi-supervised graph learning problem. We address this mapped problem by training a GCN on the high confidence voxels using the methods presented in Kipf and Welling (2017). The rest of this section describes the formulation of our partially-labeled graph.
2.2.1 Partially-Labeled Nodes
Given a graph representing our 3D volumetric data, at the inference time, we aim to obtain a refined segmentation as the results of our GCN model ,
| (4) |
where the graph is constructed from the set of volumes (see section 2.1 and Fig. 2) and represents the GCN’s parameters.
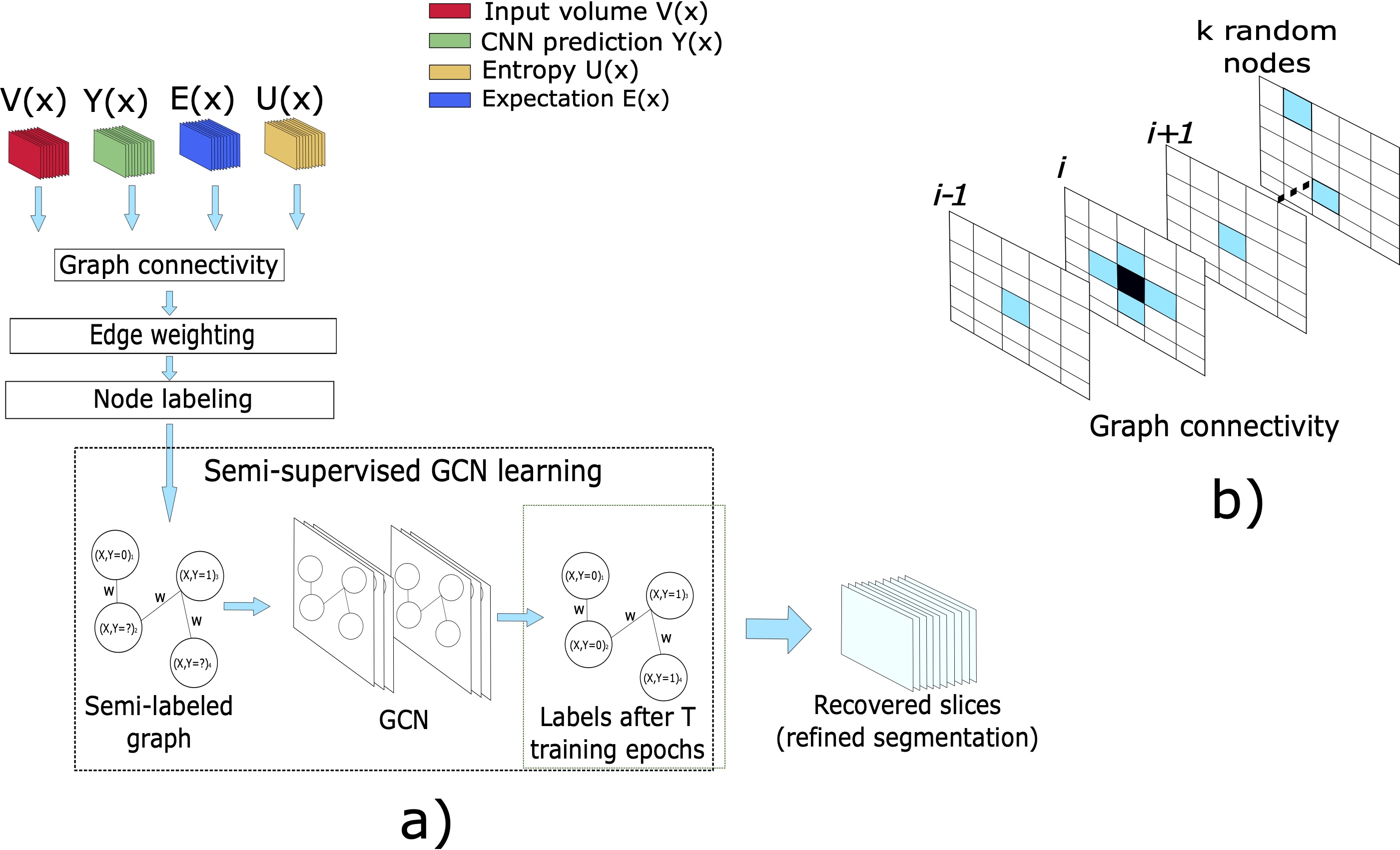
Since most of the voxels in the volume are irrelevant for the refinement process and given that graphs are not restricted to the rectangular structured representation of data, we define an ROI tailored to our target anatomy. We define our working region as with the expectation binarized by a threshold of . Since the entropy is usually high in boundary regions, including the dilated ensures that the ROI is bigger enough to contain the organ. Also, this allows us to include high confidence background predictions () for training the GCN. Including the expectation in the ROI give us high confidence foreground predictions for training the model. This ROI reduces the number of nodes of the graph and, in consequence, the memory requirements. The voxels define the nodes for . Each node is represented by a feature vector containing intensity , expectation , and entropy . Finally, we labeled each node in the graph according to its uncertainty level using the next rule:
| (5) |
2.2.2 Edges and Weighting
The most straightforward connectivity option is to consider the connectivity with adjacent voxels (n6 or n26 adjacent voxel neighborhood). However, this simple nearest neighborhood scheme may not be adequate for our problem for two reasons; First, with this scheme, every single voxel is connected with its local neighborhood but lacks global information. Considering the original volumetric representation of the data, this means that the main source of information is coming only from adjacent voxels, while information from the global context (not-adjacent voxels) is mainly ignored.
Second, voxels with high uncertainty tend to shape contiguous clusters. Because of this, a voxel with high uncertainty will be most probably surrounded by other high uncertainty points, reducing the connection with the low uncertainty points. Hence, a simple n6 or n26 connectivity might limit the propagation of information from the confidence to the uncertain regions.
A fully-connected graph can take advantage of the relationships between local and long-range connections, and propagate information from both certain and uncertain regions during training and inference time. The main disadvantage of a fully-connected graph for a GCN model is the prohibitive memory requirements.
In our work, we evaluate an intermediate solution. For a particular node (or voxel) , we create connections with its six perpendicular immediate neighbors in the volume coordinate system (N6) to consider local information. Additionally, we randomly select additional nodes in the graph and create a connection between these random elements and . This defines a sparse representation that considers local and long-range connections between high and low uncertainty elements. The random nodes can be taken from any part inside the ROI used to define the nodes of the graph. We empirically found that offers a balance in performance and graph size, and kept this value during our experiments.
To define the weights for the edges, we use a function based on Gaussian kernels considering the intensity and the 3-D position associated with the node:
| (6) |
where and are balancing factors, is given by the diversity between the nodes (Zhou et al., 2017b), defined as with , and for our binary case. We opt for an additive weighting, instead of a multiplicative one, because the GCN can take advantage of connections with both similar and dissimilar nodes (in intensity and space) in the learning process, and using a multiplicative weighting could completely cut these connections. We found out that the diversity can indirectly bring information about the similarity of two nodes, in terms of class probability.
Since the diversity does not have an upper bound, it is possible to apply a non-linear transformation in order to normalize its value to the range , leading to the following version of the diversity:
| (7) |
We can integrate this into eq.(6) replacing the regular diversity:
| (8) |
Similarly, if we only take the exponential part of eq.(7), we get a similarity metric between the expectation of the nodes and . We use this version of the diversity as a third variation of our weighting function, leading to the following expression:
| (9) |
where the function is given by
| (10) |
It is worth mentioning that if we set and keep the same value of all the weighting functions become the same.
2.2.3 Semi-Supervised GCN Learning
At this point, we have reformulated the refinement task as a semi-supervised graph learning tasks. As mentioned previously, we use the proposal from Kipf and Welling (2017) to train the GCN in a semi-supervised way. A convolutional layer is defined as:
| (11) |
The variable represents the input feature matrix of the layer with the number of nodes and the number of input features per node. is the weight matrix of the current layer with the number of output features per node. follows the renormalization proposed by Kipf and Welling (2017) with , the adjacency matrix of , and the diagonal matrix that sums across the columns of . In general, we keep the same GCN architecture, but employing a sigmoid activation function at the output layer, for binary classification. Representing our graph by its adjacency matrix and feature matrix , this leads to the following GCN model:
| (12) |
Finally, it is worth to mention that, even if we validated our proposal using this GCN learning architecture, given the modular nature of our method, it is possible to employ a different semi-supervised graph learning strategy.
3 Experiments and Results
We validate our method refining the output of a 2D CNN in the tasks of pancreas and spleen segmentation. We compare this approach with the refinement obtained from a conditional random field method (Krähenbühl and Koltun, 2011). Then, we evaluate the effects of variations in the graph-definition parameters, performing a sensitivity analysis. All the processes run on an NVidia Titan Xp. We make our code publicly available for reproducibility purposes111https://github.com/rodsom22/gcn_refinement.
3.1 Datasets
We tested our framework using two CT datasets for pancreas, and spleen segmentation. For the pancreas segmentation problem, we used the NIH pancreas dataset222https://wiki.cancerimagingarchive.net/display/Public/Pancreas-CT (Roth et al., 2016, 2015; Clark et al., 2013). We randomly selected 45 volumes of the NIH dataset for training the CNN model and reserved 20 volumes for testing the uncertainty-based GCN refinement. For spleen, we employed the spleen segmentation task of the medical segmentation decathlon (Simpson et al., 2019) (MSD-spleen333http://medicaldecathlon.com/). For this problem, we trained the CNN on 26 volumes and reserved nine volumes to test our framework. The MSD-spleen dataset contains more than one foreground label in the segmentation mask. We unified the non-background labels of the MSD-spleen dataset into a single foreground class since we evaluate our method for refining a binary segmentation model.
3.2 Implementation Details
3.2.1 CNN Baseline Model
We chose a 2D U-Net to be our CNN model (Ronneberger et al., 2015). We included dropout layers at the end of every convolutional block of the U-Net, as indicated by the MCDO method. The U-Net was trained considering a binary segmentation problem. Since we are employing a 2D model, we trained the models using axial slices. The model was trained with the dice loss function, using the Adam optimizer. We train the model for around 200 epochs keeping the overall best performing model during the entire training procedure. At inference time, we predicted every slice separately and then we stacked all the predictions together to obtain a volumetric segmentation (a similar strategy was used to perform the uncertainty analysis). As a post-processing step, we compute the largest connected component in the prediction, to reduce the number of false positives. At this point, it is worth mentioning that the U-Net was used only for testing purposes and different architectures can be used instead. This is mainly because our refinement method uses the model-independent MCDO analysis.
3.2.2 Uncertainty Analysis and GCN Implementation Details
We utilized MCDO to compute the expectation and entropy using a dropout rate of and a total of stochastic passes. To obtain volumetric uncertainty from a 2D model, we performed the uncertainty analysis on every individual slice of the input volume and then we stacked all the results together to obtain the volumetric expectation and entropy. We tested different values for the uncertainty threshold (see section 3.4.2).
The GCN model is a two-layered network with 32 feature maps in the hidden layer and a single output neuron for binary node-classification. The graphical network is trained for 200 epochs with a learning rate of , binary entropy loss, and the Adam optimizer. We kept these same settings for the refinement of both segmentation tasks. After the refinement process, we can replace only the uncertain voxels with the GCN prediction, or we can replace the entire CNN prediction with the GCN output. We use the second approach since we found it producing better results.
3.2.3 Statistical Significance Test
Given that with small sets, the statistical significance tests can fail (Szucs and Ioannidis, 2017; Biau et al., 2008), we generate the dice score in slice-wise to increase the sample size (up with 278-1700 slices for the spleen, and pancreas respectively). Then we have run the non-parametric statistical significance test, namely Kolmogorov–Smirnov test. We perform a statistical significance analysis between the results of the GCN refinement and the initial results of the CNN. A single start (*) indicates a p-value , while a double-start (**) indicates a p-value with respect to the original CNN prediction.
3.3 Comparison with State of the Art and Baseline CNN
We applied our refinement method independently on every individual sample from the 20 NIH and 9 MSD-spleen testing volumes. The edge weighting function for our refinement method is given by eq. 6 with and . Since CRF is a common refinement strategy, we use the publicly available implementation of the method presented in Krähenbühl and Koltun (2011) to refine the CNN prediction. This CRF method assumes dense connectivity. Similar to Krähenbühl and Koltun (2011), we set one unary and two pairwise potentials. We use the prediction of the CNN as the unary potential. The first pairwise potential is composed of the position of the voxel in the 3D volume. The second pairwise potential is a combination of intensity and position of the voxels. For the CRF refinement, we considered the same ROI used by the GCN.
| Task | CNN | CRF | GCN |
|---|---|---|---|
| 2D U-Net | refinement | Refinement (ours) | |
| Pancreas | * | ||
| Spleen | ** |
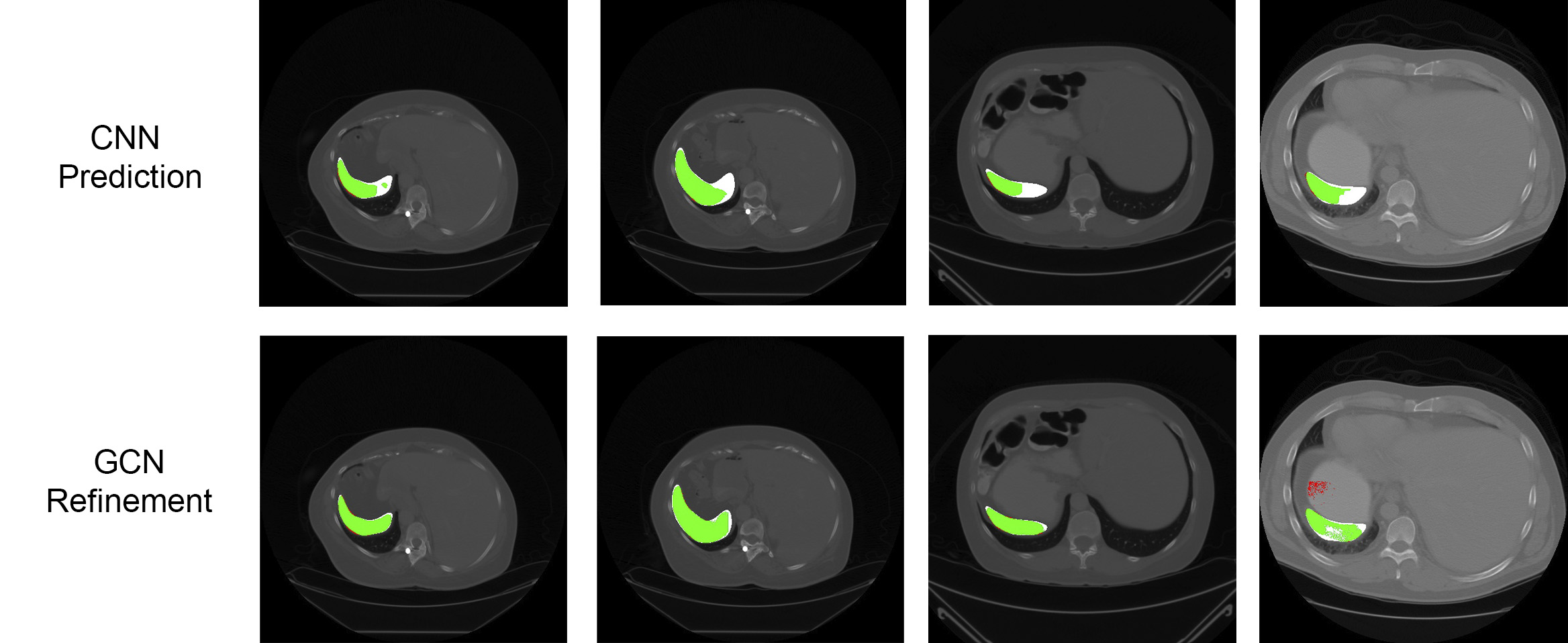
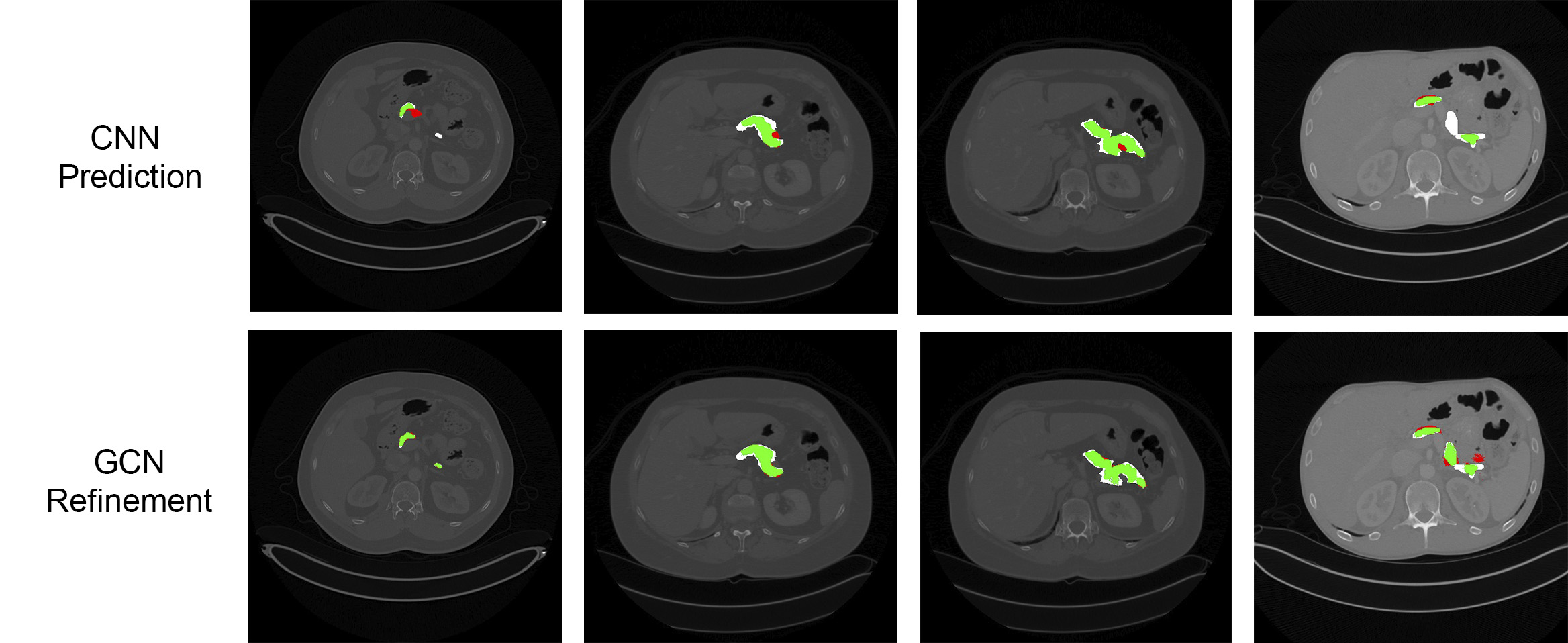
Results are presented in Table 1. The GCN-based refinement outperforms the base CNN model and the CRF refinement by around 1% and 0.6% respectively in the pancreas segmentation task. For spleen segmentation, our GCN refinement presented an increase in the dice score of 2% with respect to the base CNN, and 1.7% with respect to the CRF refinement. Figs. 3 and 4 show visual examples of the GCN refinement compared with the base CNN prediction.
3.4 Sensitivity Analysis
We performed an analysis of the performance of our proposal under different variations of their main components and hyper-parameters. Our analysis evaluate the scenario when the base CNN was trained with limited data (sec. 3.4.1). We also explore how the choice of the uncertainty threshold can affect the performance (sec. 3.4.2). A node connectivity considering the 26 surrounding neighborhood is compared with the n6 plus 16 long-range random connection we employed (sec. 3.4.3). Finally, a deep analysis on different variations of the weighting function is presented in sections 3.4.4, 3.4.5, 3.4.6, 3.4.7, and 3.4.8.
3.4.1 Influence of the Number of Training Samples
We evaluate the performance of the GCN refinement when the base CNN is trained with a small number of samples. For this, we randomly selected 10 out of the 45 training samples of the NIH dataset. For spleen, we selected nine. Results are presented in Table 2.
| Task | CNN | CRF | GCN |
|---|---|---|---|
| 2D U-Net | refinement | Refinement (ours) | |
| Pancreas-10 | * | ||
| Spleen-9 | ** |
Note the increment in the standard deviation of all the models. A reason for this can be that the CNN does not generalize adequately to the testing set, due to the small number of training examples. Similar to the previous results, the increment in the dice score for the GCN refinement is about 2.4% with respect to the CNN base model for the pancreas, and improvement of 2.3% for spleen, compared with the base CNN.
3.4.2 Influence of Uncertainty Threshold
In our experiments, we evaluate the influence of different values for . We tested the method with values of . In this way, we covered a wide range of conditions that define a voxel as “uncertain”. After training the GCN, we replaced all the CNN predictions with the GCN output. Table 3 compares the CNN output with the GCN refinement at different values of for the tasks of the pancreas and spleen segmentation.
| Task | GCN | GCN | GCN | GCN | GCN |
|---|---|---|---|---|---|
| Pancreas | |||||
| Pancreas-10 | |||||
| Spleen | |||||
| Spleen-9 |
The parameter controls the minimum requirement to consider a voxel as uncertain. Lower values lead to a higher number of uncertain elements. This has a direct relationship with the number of high certainty nodes in the graph representation, and hence, in the number of training examples for the GCN. This also influences the quality of the training voxels for the GCN, since a high threshold relaxes the amount of uncertainty necessary to rely on the prediction of the CNN.
However, from the results of Table 3, except for pancreas-10 and spleen-9, there is no significant impact on the choice of this parameter. One reason can be that there is a clear separation between high and low uncertainty points. Therefore, changing may add (remove) a few number of nodes that are insignificant for the learning process of the GCN.
For the pancreas-10 model, we notice a progressive decrease in the dice score. Since this model uses fewer training examples, it is expected to have low confidence in their predictions (in contrast with the model trained with 45 volumes). In this scenario, a higher uncertainty threshold increases the chance to include high-uncertainty nodes as ground truth for training the GCN. A lower includes fewer points but with higher confidence. This appears to be beneficial in the pancreas segmentation model trained with fewer examples.

The opposite occurs with spleen-9, where higher are beneficial. This might indicate a dependency on the characteristics of the anatomies since the pancreas presents more inter-patient and inter-slice variability (see Fig. 5).
In general, our results suggest that parameter should be selected based on the target anatomy. Further, appears to have more influence in conditions of high uncertainty, e.g. when the model is trained with fewer examples. In the cases where has no significant impact, intermediate values are preferred, since they lead to a lower number of nodes, and in consequence to lower memory requirements.
3.4.3 Node Connectivity
We compare the refinement performance of our method when a classical n26 neighborhood is employed. We repeated the experiments for different uncertainty thresholds, and the CNN model trained with different numbers of examples on the pancreas and spleen datasets. Results are presented in Tables 4 and 5 for each organ, respectively. In all tables, the weighting employed is eq. 6 with and .
| Connectivity | GCN | GCN | GCN | GCN | GCN |
|---|---|---|---|---|---|
| Ours | |||||
| n26 | |||||
| Ours-cnn10 | |||||
| n26-cnn10 |
| Connectivity | GCN | GCN | GCN | GCN | GCN |
|---|---|---|---|---|---|
| Ours | |||||
| n26 | |||||
| Ours-cnn9 | |||||
| n26-cnn9 |
The results show a better refinement when including the random long-range connections, especially when working with the CNN trained with limited data, for both tasks. It is worth to mention that when comparing with the original CNN output presented in Tables 1 and 2, our refinement method using the n26 connectivity still having a slight improvement over the original CNN prediction.
3.4.4 Edge Weighting
Finally, we analyze the influence of different variations of the components of our weighting function. We perform our refinement strategy using the weighting functions given by equations 6, 8, and 9, presented in section 2.2.2. In all the experiments of this section, we keep a fixed value of . We will use the notation , to indicate the parameters employed by the corresponding function, for example, the notation holds for weighting function with and . We explore the situations when: a) either only diversity or only the Gaussian kernels are employed (sec. 3.4.5); b) using a diversity normalized to the range [0, 1] (sec. 3.4.6); c) using similarity in expectation given by the inverse of the diversity (sec. 3.4.7); and d) we discuss deep insights regarding the three different variations of the diversity employed in the previous sections (sec. 3.4.8).
3.4.5 Weighting: Diversity and Gaussian Similarity Kernels
We can divide the weighting function into two metrics, diversity and Gaussian similarity kernels (in intensity and position). In this experiment, we keep one of these components at a time. This is done by setting the values of and to zero, accordingly. The results are presented in Table 6. Note that corresponds to the weighting function used so far.
| Task | CNN | GCN | GCN | GCN |
|---|---|---|---|---|
| 2D U-Net | ||||
| Pancreas | * | * | * | |
| Pancreas-10 | ||||
| Spleen | ** | ** | ** | |
| Spleen-9 | ** | ** | * |
Different weighting functions and variations still outperform the initial CNN prediction. Now, we will focus on the small differences between these results. As we mentioned, our weighting scheme considers diversity together with intensity and position similarity. The two later Gaussian components are commonly used in the literature and follow the intuition that two components that are similar in intensity and close to each other are likely to belong to the same class. The diversity is an additional component that allows us to include the results from the MCDO analysis in the edge weighting. The diversity has a lower bound of zero but in contrast with the Gaussian kernels, in an ideal form, it does not have an upper bound. When two nodes have a similar expectation, the diversity between those elements will be small, and the weighting function will only rely on the Gaussian similarities. When the nodes have important differences in expectation (e.g 0 vs. 1), the unbounded nature of the diversity will ignore the much smaller contribution of the Gaussian kernels (the diversity can reach values of , while each Gaussian kernel has a maximum at ), and bias the weight to the value of the diversity.
Pancreas models.
In a high-training-data scenario, a Gaussian-kernel-only () scheme appears to be good enough for the refinement strategy. In the low data-regime, the GCN appears to take more advantage of diversity. Our features employ intensity, expectation, and entropy (or uncertainty). Note that the uncertainty threshold affects the labeled nodes but does not affect the connectivity. A node can be connected to any certain or uncertain neighbor, and a Gaussian-kernel-only weighting is not aware of possible inconsistencies in the node features.
Spleen models.
The spleen segmentation problem shows different behavior. The lower inter-patient variability of the spleen could be a reason (see Figs. 5). In a high-training-data regime, it can bring a more stable and well-separated expectation between organ and background, making the diversity a more favorable weighting. In a low data regime, the Gaussian-kernel-only version appears to perform better. However, from Table 3, a larger appears to benefit the low-data spleen problem. In fact, at , the dice-score for and are 81.09, and 81.15, respectively, showing no significant difference. Note that .
3.4.6 Normalizing the Diversity
One of the questions, we had, during this work whether the normalization of the diversity would have a positive/negative impact on the behavior of the GCN. In fact, presents a negative impact on the learning process. As we mentioned, the unbounded nature of the diversity makes to prefer connections with opposed expectations (and ignore the Gaussian similarity in those cases). On the other hand, the Gaussian similarity is only considered when the expectation of both nodes is basically the same, and even in those cases, the weight is small compared with the values of the diversity. In this sense, the GCN can learn mostly from examples that are different in expectation or (with a considerably lower contribution ) from examples similar in intensity and position.
Using , which normalizes the diversity into a value between 0 and 1, makes the contribution of the Gaussian kernels more representative. The normalized diversity of will no longer ignore the Gaussian similarity, and it will assign the highest weights to connections between nodes that are similar in intensity and position, but at the same time different in expectation, which is counter-intuitive. Table 7 shows the drop in the performance using as weighting function. Given that the diversity is in range between 0 and 1, we use for .
| Task | CNN | GCN | GCN |
|---|---|---|---|
| 2D U-Net | |||
| Pancreas | * | ** | |
| Pancreas-10 | ** | ||
| Spleen | ** | ** | |
| Spleen-9 | ** | ** |
3.4.7 All-Similarity Weighting
If we take only the exponential part of eq. 7, we will obtain values in the range [0,1] that gives high weights to similar expectations, presenting a better agreement with the Gaussian kernels. This weighting scheme is given by . The results, compared with the U-Net and the initial weighting function are presented in Table 8. Results, again show an improvement for the GCN refinement, supporting our discussion about .
| Task | CNN | GCN | GCN |
|---|---|---|---|
| 2D U-Net | |||
| Pancreas | * | * | |
| Pancreas-10 | |||
| Spleen | ** | ** | |
| Spleen-9 | ** | ** |
Pancreas models.
Again, we can first focus on the results of the pancreas. The inverse of the diversity in combination with the Gaussian kernels appears to perform well with the pancreas model trained with a high number of examples. This can be because of the number of examples is enough to derive a good estimation of the expectation, in contrast with the low-data pancreas U-Net.
Spleen models.
For the spleen problem, the differences appear to be not significant. In general, the results suggest that is beneficial for the full-data pancreas problem, and does work well with both spleen models. But might be sub-optimal for the low-data pancreas refinement task. A possible explanation is that will assign high weights to nodes with similar values, no matter if both have expectations of 1, 0, or 0.5. This last expectation value (0.5) represents a high uncertainty point, and it is expected to find this kind of point on an irregular organ, and with a model trained with a low number of examples, like Pancreas-10. In this sense, the inverse of the diversity in might also assign a high weight to connections between uncertainty nodes.
3.4.8 Diversity-Only Weighting
In this section, as final analysis for the weighting function, we compare , , and when . The results are presented in Table 9. Two points are worth mentioning. Comparing the results of in Table 9 with the results of in Table 7, it is clear that the only-diversity version of has better performance, supporting the idea of the inconsistent connections of .
| Task | CNN | GCN | GCN | GCN |
|---|---|---|---|---|
| 2D U-Net | ||||
| Pancreas | * | ** | * | |
| Pancreas-10 | * | |||
| Spleen | ** | ** | ** | |
| Spleen-9 | ** | * |
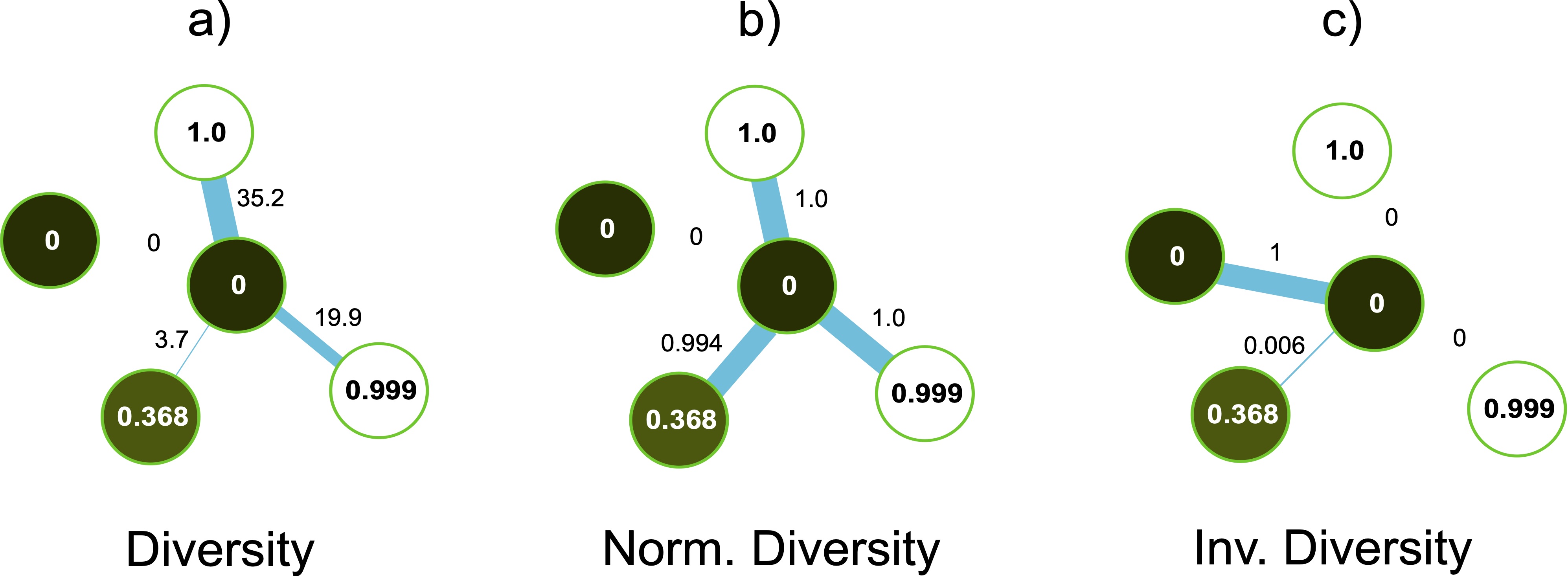
The second interesting fact comes when comparing the diversity of with the normalized diversity of , both in Table 9. Even though these two functions are expected to behave similarly, we notice a difference in their performance. To understand the possible causes of these differences, we take a closer look at the assigned weights of these functions to a subset of nodes. Let’s consider a central node with expectation close to zero, and four neighbors nodes with expectations of approximately 0.0, 1.0, 0.999, and 0.368, respectively (see Fig. 6). As expected, will assign high values to opposed expectations (36.2 and 19.9 in Figure 6.a), while the weight will be low for similar expectations, and close to zero to identical expectations (weights of 3.7 and 0 in Fig. 6.a). However, for the same node structure, will weight with a high value (close to 1) almost all the connections, except for the neighbors with the same expectation (see Fig, 6.b). Even though the difference between the expectations values of 1 and 0.368 is not high enough, will give an importance that is similar to the nodes with completely opposed expectations, leading to an inconsistent weighting scheme. In contrast, (which acts as a kind of similarity in expectation) assigns weights close to zero to all the nodes that do not have the same expectation, even to the pair (0, 0.368), see Fig. 6.c. This can suggest a better consistency for the inverse diversity, compared with diversity normalized to [0, 1].
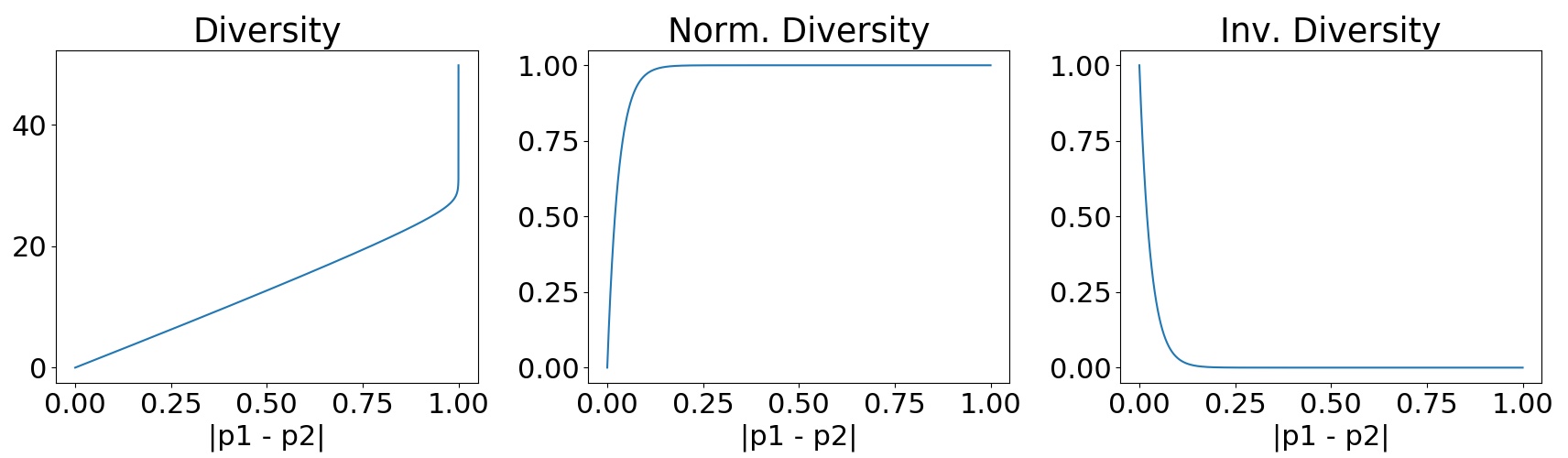
We can also see these conclusions if we plot the values for these three variations of the diversity as a function of the difference between and (see Fig. 7). We can see how the diversity grows exponentially when the difference between and is close to 1 (Fig. 7 Diversity). In a similar way, the inverse diversity assigns a weight of 1 to differences close to zero and decreases exponentially at the moment this difference starts to increment (Fig. 7 Inv. Diversity). Finally, the normalized diversity starts assigning a weight of zero to equal expectations, however, the curve grows exponentially until reaching a weight of 1 when the difference in expectations still close to 0.2 (Fig. 7 Norm. Diversity), leading to the inconsistencies mentioned before.
In general, a weighting function like appears to be not recommendable for the refinement with GCNs. The inverse diversity of can be a better option, however, it is also possible that under certain conditions, this weighting could introduce noisy connections. For example, when the expectation has values close to 0.5 for both nodes, the function will assign high weights, however, this might not heavily contribute to the GCN given the fact that these nodes might have high uncertainty as well. This suggests that, under high uncertainty environments, it is better to weigh based on dissimilarity in expectation. On the other hand, the inverse of diversity can take advantage of well-separated expectations.
3.5 Hyper-parameters Search
We performed an exhaustive search across the different weighting functions, and uncertainty thresholds, leading to the results presented in Table 10.
As noted, the improvements are not significantly different from the initial weighting function presented in our initial work (Soberanis-Mukul et al., 2020), which suggests that this weighting function is good enough for the presented tasks. Nevertheless, a hyper-parameter search, e.g. choice of the weighting function, and , might lead to better performance. This mainly depends on the structure of interest and its characteristics, though.
| Task | CNN | GCN (Soberanis-Mukul et al., 2020) | GCN |
|---|---|---|---|
| 2D U-Net | updated scores | ||
| Pancreas | * () | * (, ) | |
| Pancreas-10 | * () | * (, ) | |
| Spleen | ** () | ** (, ) | |
| Spleen-9 | ** () | * (, ) |
3.6 Deep Insights on Prediction, Expectation, and Entropy
We employed three elements from the uncertainty analysis in the definition of our graph: the CNN’s prediction, the CNN’s expectation, and the CNN’s entropy. Fig. 8 shows an example of these components.

The labels of the graph are given by the CNN’s high-confidence prediction. However, from Fig. 8 we can see that the refinement is similar to the expectation. The expectation is one of the features of the nodes. Also is the main component for the diversity in the edge’s weighting function (see section 2.2.2). The GCN can learn how to use the CNN’s expectation, together with intensity and spatial information, to reclassify the nodes of the graph. However, it can also generate false positives if the expectation contains artifacts. Fig. 8 shows an example of this case, where we can see a region in the expectation that does not agree with the ground truth. It can be also noticed that the GCN reduced this region. This can be a result of the random long-range connections included in the graph definition.
In our last experiment, we evaluate the relationship between the expectation and the GCN refinement. For this, we compute the relative improvement between the GCN and the expectation. First, the expectation was thresholded by 0.5. Then we computed its dice score with the ground truth. The relative improvement is computed as:
| (13) |
We compute for every input volume. Fig. 9 shows the results for the pancreas segmentation task, and compares the metric when the expectation was obtained from a model trained with 45 (Fig.9a) and 10 samples (Fig.9b), respectively, for pancreas segmentation.

Fig. 9a shows that most of DICE coefficients (17/20) of the GCN refinement are either below or close to the ones of the expectation. However, three volumes show an improvement in the DICE compared to the expectation. This is different in Fig. 9b. Here, (13/20) volumes show either better or similar DICE for the GCN compared to the expectation. A possible explanation is that models trained with an adequate number of examples (volumes), their expectation is good enough. In contrast, models trained with a few examples (volumes) have higher uncertainties yielding unreliable expectations. Our results suggest that our GCN refinement strategy is favorable over the expectation or uncertainty analysis in such scenarios.
3.7 Applicability to other network architectures
As a refinement strategy, our proposed method is orthogonal to any segmentation pipeline and can be applied to different CNNs architectures equipped with the MDCO approximation. To verify this, we apply the uncertainty-GCN refinement to the predictions of QuickNat (Roy et al., 2019b, a), trained on the same two segmentation tasks. The network is trained using the same 45 volumes for the pancreas, and 26 for the spleen, under similar settings as the U-Net. The testing set is the same we used to evaluate the GCN refinement from U-Net. We employed the weighting function with and for the pancreas and spleen models, respectively. Table 11 presents the results for the initial QuickNat prediction and the GCN refinement.
| Task | 3D U-Net | 2D U-Net | Ours | 2D QuickNat | Ours |
| Initial | GCN-Refinement | Initial | GCN-Refinement | ||
| Pancreas | * | ||||
| Spleen | ** |
Reported results show an improvement over the initial CNN model but on a different level compared to the results obtained with the U-Net. While the spleen problem shows an improvement of over the initial prediction, the pancreas model shows subtle changes. Such differences among different CNNs can be attributed to the epistemic uncertainty inherent to their respective models. In other words, different behaviors of the uncertainty across models can lead to different behaviors in the GCN refinement strategy. However, a deeper analysis of inter-model uncertainty and their relationship with the Graph-based refinement is necessary.
3.8 2D vs. 3D Architectures
In our experiments, we employed a 2D architecture since it provides us with all the necessary components to test our method. Nevertheless, our refinement strategy is orthogonal to other segmentation approaches and can be applied to any CNN that produces uncertainty measures with MCDO. This also includes 3D models. However, to our best knowledge, MCDO is most commonly employed with 2D models and its translation to 3D might require additional methodological efforts derived from working with 3D architectures together with additional requirements for data-handling due to memory constraints (LaBonte et al., 2019). Further, 3D model might not necessarily provide a better initial segmentation compared to a 2D CNN as reported by Zhou et al. (2019); Wang et al. (2019). In this regard, we trained a standard 3D U-Net (Oktay et al., 2018) subdividing the input volume into blocks of , with a minimum feature size of 16 for the U-Net convolutions. This allows us to use batches of 8 during training on a NVidia Titan Xp of 12 GB. This lead to a dice-score of for the pancreas segmentation problem, and for the spleen segmentation, using the same training, and testing set as the 2D U-Nets (see Table 11). As can be seen, under similar conditions, the 3D model presents a lower performance compared with their 2D counterparts. This can be due to the loss of the global context derived from the subdivision of the volume. Fit the entire volume can contribute to the performance. However, this can be limited by the current GPU memory capabilities. Similarly, using a volume-level input will reduce the number of available samples, which can lead to overfitting problems. Even though we are aware of U-Net, V-Net inspired 3D architectures defined for pancreas segmentation that can reach around of dice score, with the use of data augmentation and auxiliary losses for deep supervision (Zhu et al., 2018), or fine-tuning with the addition of attention gates (Oktay et al., 2018), we consider that the 2D U-Net gives us good-enough results on both segmentation problems with an appropriate simplicity to evaluate our framework. Nevertheless, investigating our approach using 3D models equipped with MCDO might be an interesting direction.
4 Discussion and Conclusion
In this work, we have presented a method to construct a sparse semi-labeled graph representation of volumetric medical data, based on the output and uncertainty analysis of a CNN model. We have also shown that graph semi-supervised learning can be used to obtain a refined segmentation. We also provided a deep analysis of the weighting function employed to construct the graph. We have shown that diversity is an adequate choice for expectation-based edge weighting. In a similar way, the inverse diversity can also be a good option under certain circumstances. The dependence of the graph to the expectation and the uncertainty analysis method employed could explain the differences in the performance when refining the prediction of two different CNNs. In this regard, alternatives to the uncertainty estimation method, and the use of calibrated uncertainties can be an interesting direction when working with different CNNs models.
Computational Time:
Regarding computational time, our method requires to define a graph and then train a GCN model. This can require more computational requirements compared with the most efficient versions of CRF. In our experiments, the time required for training and testing the GCN in the constructed graph is around twice the time required for CRF in the fully connected version of our uncertainty graph. This is a time of around 30 sec 1 min for the GCN vs. 13 sec 30 sec for CRF. These numbers do not consider the time for uncertainty analysis and graph construction.
Early Stopping Criteria for the CNN:
Our method is intended for refining a CNN model training with a standard procedure. It is not trained in an end-to-end fashion (jointly with the CNN). Applying an early stopping criterion could have as a consequence an increase in the uncertainty area, generating a bigger ROI, increasing the number of nodes and, hence, increasing the memory requirements for the GCN.
Uncertainty Quantification:
In this work, we have employed MCDO (Kendall and Gal, 2017) for the model uncertainty analysis, and found out the expectation could be a good choice for well-trained models, while our GCN refinement shows superior performance, compared to the expectation, in low-data regime. Nonetheless, recently proposed uncertainty measures (Tomczack et al., 2019), which disentangle the model’s uncertainty from the one associated with the inter/intra-observer variability, might be desirable.
Graph Representation:
We have investigated different connectivity and weighting mechanisms in defining our graph and extracted a couple of features to represent our nodes. However, prior knowledge, e.g. geometry, could be used to constrain the ROI and provide plausible configurations (Degel et al., 2018; Oktay et al., 2017).
Large Organs and Multi-class Segmentation:
We have shown that the model can be applied to different organ segmentation problems and CNN architectures. Similarly, our results suggest that the performance can depend on the characteristics of the anatomy studied. In this sense, large and stable organs like the liver can derive in performance similar to the spleen. However, further experiments are necessary to verify this. Similarly, large organs can represent a challenge for a graph-based method, since a graph constructed over voxels can lead to high memory requirements. A change on the node representation of the CT data can help in this problem, however, we leave this as future work. In this work, we addressed a binary classification problem. For a multi-class problem, it should be possible to obtain a vectorial expectation representing each class, and the entropy can be computed considering multiple classes. Even though this brings all the elements to formulate the partially labeled graph, given the complexity in the different structures that share intensity similarities between tissues, a different weighting, connectivity, and node features might be necessary to include meaningful information about the anatomies. Similarly, the inclusion of a larger number of structures will lead to a larger number of nodes, making the efficient node representation of multi-class data an interesting future direction.
Acknowledgments
R. D. S. was supported by Consejo Nacional de Ciencia y Tecnología (CONACYT), Mexico. S.A. was supported by the PRIME programme of the German Academic Exchange Service (DAAD) with funds from the German Federal Ministry of Education and Research (BMBF) when he contributed to this work.
Ethical Standards
The work follows appropriate ethical standards in conducting research and writing the manuscript. This work presents computational models trained with publicly available data, for which no ethical approval was required.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bai et al. (2017) Wenjia Bai, Ozan Oktay, Matthew Sinclair, Hideaki Suzuki, Martin Rajchl, Giacomo Tarroni, Ben Glocker, Andrew King, Paul M. Matthews, and Daniel Rueckert. Semi-supervised learning for network-based cardiac mr image segmentation. In Medical Image Computing and Computer Assisted Intervention (MICCAI), 2017.
- Biau et al. (2008) David Jean Biau, Solen Kernéis, and Raphaël Porcher. Statistics in brief: the importance of sample size in the planning and interpretation of medical research. Clinical orthopaedics and related research, 2008.
- Clark et al. (2013) Kenneth Clark, Bruce Vendt, Kirk Smith, John Freymann, Justin Kirby, Paul Koppel, Stephen Moore, Stanley Phillips, David Maffitt, Michael Pringle, Lawrence Tarbox, and Fred Prior. The cancer imaging archive (tcia): Maintaining and operating a public information repository. Journal of Digital Imaging, 2013.
- Degel et al. (2018) Markus A Degel, Nassir Navab, and Shadi Albarqouni. Domain and geometry agnostic cnns for left atrium segmentation in 3d ultrasound. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 630–637. Springer, 2018.
- Dias and Medeiros (2019) Philipe Ambrozio Dias and Henry Medeiros. Semantic segmentation refinement by monte carlo region growing of high confidence detections. In Asian Conference on Computer Vision (ACCV), 2019.
- Gal and Ghahramani (2016) Yarin Gal and Zoubin Ghahramani. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the 33 rd International Conference on Machine Learning, 2016.
- Juarez et al. (2019) Antonio Garcia-Uceda Juarez, Raghavendra Selvan, Zaigham Saghir, and Marleen de Bruijne. A joint 3d unet-graph neural network-based method for airway segmentation from chest cts. In Machine Learning in Medical Imaging. Springer, 2019.
- Kamnitsas et al. (2017) Konstantinos Kamnitsas, Christian Ledig, Virginia F.J. Newcombe, Joanna P. Simpson, Andrew D. Kane, David K. Menon, Daniel Rueckert, and Ben Glocker. Efficient multi-scale 3d cnn with fully connected crf for accurate brain lesion segmentation. Medical Image Analysis, 2017.
- Kendall and Gal (2017) Alex Kendall and Yarin Gal. What uncertainties do we need in bayesian deep learning for computer vision? In Proceedings of the 31th International Conference on Neural Information Processing Systems (NIPS), 2017.
- Kipf and Welling (2017) Thomas N. Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations (ICLR), 2017.
- Krähenbühl and Koltun (2011) Philip Krähenbühl and Vladlen Koltun. Efficient inference in fully connected crfs with gaussian edge potentials. In Proceedings of the 24th International Conference on Neural Information Processing Systems (NIPS), 2011.
- LaBonte et al. (2019) Tyler LaBonte, Carianne Martinez, and Scott Roberts. We know where we don’t know: 3d bayesian cnns for credible geometric uncertainty. arXiv:1910.10793, 2019.
- Li and Ping (2018) Yi Li and Wei Ping. Cancer metastasis detection with neural conditional random field. In 1st Conference on Medical Imaging with Deep Learning (MIDL 2018), 2018.
- Nair et al. (2018) Tanya Nair, Doina Precup, Douglas L. Arnold, and Tal Arbel. Exploring uncertainty measures in deep networks for multiple sclerosis lesion detection and segmentation. In Medical Image Computing and Computer Assisted Intervention (MICCAI), 2018.
- Oktay et al. (2017) Ozan Oktay, Enzo Ferrante, Konstantinos Kamnitsas, Mattias Heinrich, Wenjia Bai, Jose Caballero, Stuart A Cook, Antonio De Marvao, Timothy Dawes, Declan P O‘Regan, et al. Anatomically constrained neural networks (acnns): application to cardiac image enhancement and segmentation. IEEE transactions on medical imaging, 37(2):384–395, 2017.
- Oktay et al. (2018) Ozan Oktay, Jo Schlemper, Loic Le Folgoc, Matthew Lee, Mattias Heinrich, Kazunari Misawa, Kensaku Mori, Steven McDonagh, Nils Y Hammerla, Bernhard Kainz, Ben Glocker, and Daniel Rueckert1. Attention u-net: Learning where to look for the pancreas. In 1st Conference on Medical Imaging with Deep Learning (MIDL 2018), 2018.
- Ronneberger et al. (2015) Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer Assisted Intervention (MICCAI), 2015.
- Roth et al. (2018) Holger Roth, Masahiro Oda, Natsuki Shimizu, Hirohisa Oda, Yuichiro Hayashi, Takayuki Kitasaka, Michitaka Fujiwara, Kazunari Misawa, and Kensaku Mori. Towards dense volumetric pancreas segmentation in ct using 3d fully convolutional networks. In SPIE Medical Imaging 2018, 2018.
- Roth et al. (2015) Holger R. Roth, Le Lu, Amal Farag, Hoo-Chang Shin, Jiamin Liu, Evrim Turkbey, and Ronald M. Summers. Deeporgan: Multi-level deep convolutional networks for automated pancreas segmentation. In Medical Image Computing and Computer Assisted Intervention (MICCAI), 2015.
- Roth et al. (2016) Holger R. Roth, Amal Farag, Evrim B. Turkbey, Le Lu, Jiamin Liu, and Ronald M. Summers. Data from pancreas-ct. the cancer imaging archive. http://doi.org/10.7937/K9/TCIA.2016.tNB1kqBU, 2016.
- Roy et al. (2019a) Abhijit Guha Roy, Sailesh Conjeti, Nassir Navab, Christian Wachinger, Alzheimer’s Disease Neuroimaging Initiative, et al. Bayesian quicknat: Model uncertainty in deep whole-brain segmentation for structure-wise quality control. NeuroImage, 195:11–22, 2019a.
- Roy et al. (2019b) Abhijit Guha Roy, Sailesh Conjeti, Nassir Navab, Christian Wachinger, Alzheimer’s Disease Neuroimaging Initiative, et al. Quicknat: A fully convolutional network for quick and accurate segmentation of neuroanatomy. NeuroImage, 186:713–727, 2019b.
- Selvan et al. (2018) Raghavendra Selvan, Thomas Kipf, Max Welling, Jesper H. Pedersen, Jens Petersen, and Marleen de Bruijne. Extraction of airways using graph neural networks. In 1st Conference on Medical Imaging with Deep Learning (MIDL 2018), 2018.
- Shin et al. (2019) Seung Yeon Shin, Soochahn Lee, Il Dong Yun, and Kyoung Mu Lee. Deep vessel segmentation by learning graphical connectivity. Medical Image Analysis, 2019.
- Simpson et al. (2019) Amber L. Simpson, Michela Antonelli, Spyridon Bakas, Michel Bilello, Keyvan Farahani, Bram van Ginneken, Annette Kopp-Schneider, Bennett A. Landman, Geert Litjens, Bjoern Menze, Olaf Ronneberger, Ronald M. Summers, Patrick Bilic, Patrick F. Christ, Richard K. G. Do, Marc Gollub, Jennifer Golia-Pernicka, Stephan H. Heckers, William R. Jarnagin, Maureen K. McHugo, Sandy Napel, Eugene Vorontsov, Lena Maier-Hein, and M. Jorge Cardoso. A large annotated medical image dataset for the development and evaluation of segmentation algorithms. arXiv:1902.09063, 2019.
- Soberanis-Mukul et al. (2020) Roger D. Soberanis-Mukul, Nassir Navab, and Shadi Albarqouni. Uncertainty-based graph convolutional networks for organ segmentation refinement. In International Conference on Medical Imaging with Deep Learning (MIDL 2020), 2020.
- Szucs and Ioannidis (2017) Debes Szucs and John P. A. Ioannidis. When null hypothesis significance testing is unsuitable for research: A reassessment. Frontiers in Human Neuroscience, 2017.
- Tomczack et al. (2019) Agnieszka Tomczack, Nassir Navab, and Shadi Albarqouni. Learn to estimate labels uncertainty for quality assurance. arXiv preprint arXiv:1909.08058, 2019.
- Wang et al. (2018) Guotai Wang, Wenqi Li, Maria A. Zuluaga, Rosalind Pratt, Premal A. Patel, Michael Aertsen, Tom Doel, Anna L. David, Jan Deprest, Sebastien Ourselin, and Tom Vercauteren. Interactive medical image segmentation using deep learning with image-specific fine tuning. IEEE Transactions on Medical Imaging, 2018.
- Wang et al. (2019) Yan Wang, Yuyin Zhou, Wei Shen, Seyoun Park, Elliot K. Fishman, and Alan L. Yuille. Abdominal multi-organ segmentation with organ-attention networks and statistical fusion. Medical image analysis, 55, 2019.
- Xia et al. (2018) Yingda Xia, Fengze Liu, Dong Yang, Jinzheng Cai, Lequan Yu, Zhuotun Zhu, Daguang Xu, Alan Yuille, and Holger Roth. 3d semi-supervised learning with uncertainty-aware multi-view co-training. arXiv:1811.12506, 2018.
- Yao et al. (2019) Jiawen Yao, Jinzheng Cai, Dong Yang, Daguang Xu, and Junzhou Huang. Integrating 3d geometry of organ for improving medical image segmentation. In Medical Image Computing and Computer Assisted Intervention (MICCAI), 2019.
- Yu et al. (2019) Lequan Yu, Shujun Wang, Xiaomeng Li, Chi-Wing Fu, and Pheng-Ann Heng. Uncertainty-aware self-ensembling model for semi-supervised 3d left atrium segmentation. In Medical Image Computing and Computer Assisted Intervention (MICCAI), 2019.
- Yushkevich et al. (2006) Paul A. Yushkevich, Joseph Piven, Heather Cody Hazlett, Rachel Gimpel Smith, Sean Ho, James C. Gee, and Guido Gerig. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage, 31(3):1116–1128, 2006.
- Zhou et al. (2017a) Yuyin Zhou, Lingxi Xie, Wei Shen, Yan Wang, Elliot K. Fishman, and Alan L. Yuille. A fixed-point model for pancreas segmentation in abdominal ct scans. In Medical Image Computing and Computer Assisted Intervention (MICCAI), 2017a.
- Zhou et al. (2019) Yuyin Zhou, Zhe Li, Song Bai, Chong Wang, Xinlei Chen, Mei Han, Elliot K. Fishman, and Alan L. Yuille. Prior-aware neural network for partially-supervised multi-organ segmentation. 2019 IEEE/CVF International Conference on Computer Vision (ICCV), pages 10671–10680, 2019.
- Zhou et al. (2017b) Zongwei Zhou, Jae Shin, Lei Zhang, Suryakanth Gurudu, Michael Gotway, and Jianming Liang. Fine-tuning convolutional neural networks for biomedical image analysis: Actively and incrementally. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017b.
- Zhu et al. (2018) Zhuotun Zhu, Yingda Xia, Wei Shen, Elliot K. Fishman, and Alan L. Yuille. A 3d coarse-to-fine framework for volumetric medical image segmentation. In 2018 International Conference on 3D Vision (3DV), 2018.

