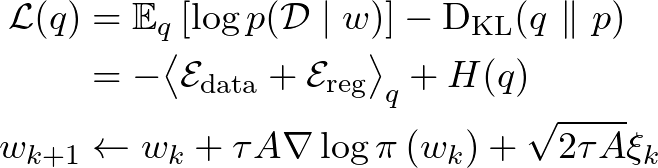1 Introduction
Image registration is the problem of aligning images into a common coordinate system such that the discrete pixel locations have the same semantic information. It is a common pre-processing step for many applications, e.g. the statistical analysis of imaging data and computer-aided diagnosis through comparison with an atlas. Image registration methods based on deep learning tend to incorporate task-specific knowledge from large datasets, whereas traditional methods are more general purpose. Many established models are based on the iterative optimisation of an energy function consisting of task-specific similarity and regularisation terms, which has to be done independently for every pair of images in order to calculate the deformation field (Schnabel2001; Klein2009; Avants2014).
DLIR (DeVos2019) and VoxelMorph (Balakrishnan2018; Balakrishnan2019; Dalca2018; Dalca2019) changed this paradigm by learning a function that maps a pair of input images to a deformation field. This gives a speed-up of several orders of magnitude at inference time and maintains an accuracy comparable to traditional methods. An overview of state-of-the-art models for image registration based on deep learning can be found in Lee2019.
Due to the perceived conceptual difficulty and computational overhead, Bayesian methods tend to be shunned when designing medical image analysis algorithms. However, in order to fully explore the parameter space and lessen the impact of ad-hoc hyperparameter choices, it is desirable to use Bayesian models. In addition, with help of open-source libraries with automatic differentiation like PyTorch, the implementation of even complex Bayesian models for image registration is very similar to that of non-probabilistic models.
In this paper, we make use of the stochastic gradient Markov chain Monte Carlo (SG-MCMC)algorithm to design an efficient posterior sampling algorithm for 3D non-rigid image registration. SG-MCMCis based on the idea of stochastic gradient descent interpreted as a stochastic process with a stationary distribution centred on the optimum and whose covariance can be used to approximate the posterior distribution (Chen2016; Mandt2017). SG-MCMCmethods have been useful for training generative models on very large datasets ubiquitous in computer vision, e.g. Du2019; Nijkamp2019; Zhang2020. We show that they are also applicable to image registration.
This work is an extended version of Grzech2020, where we first proposed use of the SG-MCMCalgorithm for non-rigid image registration. The code to reproduce the results is available in a public repository: https://github.com/dgrzech/ir-sgmcmc. The following is a summary of the main contributions of the previous work:
- 1.
We proposed a computationally efficient SG-MCMCalgorithm for three-dimensional diffeomorphic non-rigid image registration;
- 2.
We introduced a new regularisation loss, which allows to carry out inference of the regularisation strength when using a transformation parametrisation with a large number of degrees of freedom;
- 3.
We evaluated the model both qualitatively and quantitatively by analysing the output transformations, image registration accuracy, and uncertainty estimates on inter-subject brain magnetic resonance imaging (MRI)data from the UK Biobank dataset.
In this version, we extend the previous work:
- –
We provide more details on the Bayesian formulation, including a comprehensive analysis of the learnable regularisation loss, as well as a more in-depth analysis of the model hyperparameters and hyperpriors;
- –
We conduct additional experiments in order to compare the uncertainty estimates output by variational inference (VI), SG-MCMC, and VoxelMorph qualitatively, as well as quantitatively by analysing the Pearson correlation coefficient between the displacement and label uncertainties;
- –
We analyse the differences between uncertainty estimates when the SG-MCMCalgorithm is initialised to different transformations and when using different parametrisations of the transformation, including non-parametric stationary velocity fields (SVFs)and SVFsbased on B-splines; and
- –
We include a detailed evaluation of the computational speed and of the output transformation smoothness.
2 Related work
The problem of uncertainty quantification in non-rigid image registration is controversial because of ambiguity regarding the definition of uncertainty as well as the accuracy of uncertainty estimates (Luo2019). Uncertainty quantification in probabilistic image registration relies either on variational Bayesian methods (Simpson2012; Simpson2013; Wassermann2014), which are fast and approximate, and popular within models based on deep learning (Dalca2018; Liu2019; Schultz2019), or Markov chain Monte Carlo (MCMC)methods, which are slower but enable asymptotically exact sampling from the posterior distribution of the transformation parameters. The latter include e.g. Metropolis-Hastings used for intra-subject registration of brain MRIscans (Risholm2010; Risholm2013) and estimating delivery dose in radiotherapy (Risholm2011), reversible-jump MCMCused for cardiac MRI(LeFolgoc2017), and Hamiltonian Monte Carlo used for atlas building (Zhang2013).
Uncertainty quantification for image registration has also been done via kernel regression (Zollei2007; Firdaus2012) and deep learning (Dalca2018; Krebs2019; Heinrich2019; Sedghi2019). More generally, Bayesian frameworks have been used e.g. to characterize image intensities (Hachama2012) and anatomic variability (Zhang2014).
One of the main obstacles to a more widespread use of MCMCmethods for uncertainty quantification is the computational cost. This was recently tackled by embedding MCMCin a multilevel framework (Schultz2018). SG-MCMCwas previously used for rigid image registration (Karabulut2017). It has also been employed in the context of unsupervised non-rigid image registration based on deep learning, where it allowed to sample from the posterior distribution of the network weights, rather than directly the transformation parameters (Khawaled2020).
Previous work on data-driven regularisation focuses on transformation parametrisations with a relatively low number of degrees of freedom, e.g. B-splines (Simpson2012) and a sparse parametrisation based on Gaussian radial basis functions (RBFs)(LeFolgoc2017). Limited work exists also on spatially-varying regularisation, again with B-splines (Simpson2015). Deep learning has been used for spatially-varying regularisation learnt using more than one image pair (Niethammer2019). Shen2019 introduced a related model which could be used for learning regularisation strength based on a single image pair but suffered from non-diffeomorphic output transformations and slow speed.
3 Registration model
We denote an image pair by , where and are a fixed and a moving image respectively. The goal of image registration is to align the underlying domains and with a transformation , i.e. to calculate parameters such that . The transformation is often expected to possess desirable properties, e.g. diffeomorphic transformations are smooth and invertible, with a smooth inverse.
We parametrise the transformation using the SVFformulation (Arsigny2006; Ashburner2007), which we briefly review below. The ordinary differential equation (ODE)that defines the evolution of the transformation is given by:
| (1) |
where is the identity transformation and . If the velocity field is spatially smooth, then the solution to Equation 1 is a diffeomorphic transformation. Numerical integration is done by scaling and squaring, which uses the following recurrence relation with steps (Arsigny2006):
| (2) |
The Bayesian image registration framework that we present is not limited to SVFs. Moreover, there is a very limited amount of research on the impact of the transformation parametrisation on uncertainty quantification. Previous work on uncertainty quantification in image registration characterised uncertainty using a single transformation parametrisation, e.g. a small deformation model using B-splines in Simpson2012, the finite element (FE)method in Risholm2013, and multi-scale Gaussian RBFsin LeFolgoc2017, or a large deformation diffeomorphic metric mapping (LDDMM)in Wassermann2014.
To help understand the potential impact of the transformation parametrisation on uncertainty quantification, we also implement SVFsbased on cubic B-splines (Modat2012). In this case, the SVFconsists of a grid of B-spline control points, with regular spacing voxel. The dense SVFat each point is a weighted combination of cubic B-spline basis functions (Rueckert1999). To calculate the transformation based on the dense velocity field, we again use the scaling and squaring algorithm in Equation 2.
3.1 Likelihood model
The likelihood specifies the relationship between the data and the transformation parameters by means of a similarity metric. In probabilistic image registration, it usually takes the form of a Boltzmann distribution (Ashburner2007):
| (3) |
where is the similarity metric and an optional set of hyperparameters.