A Review of Causality for Learning Algorithms in Medical Image Analysis

Vlontzos, Athanasios; Rueckert, Daniel; Kainz, Bernhard

doi:https://doi.org/10.59275/j.melba.2022-4gf2

1 Introduction

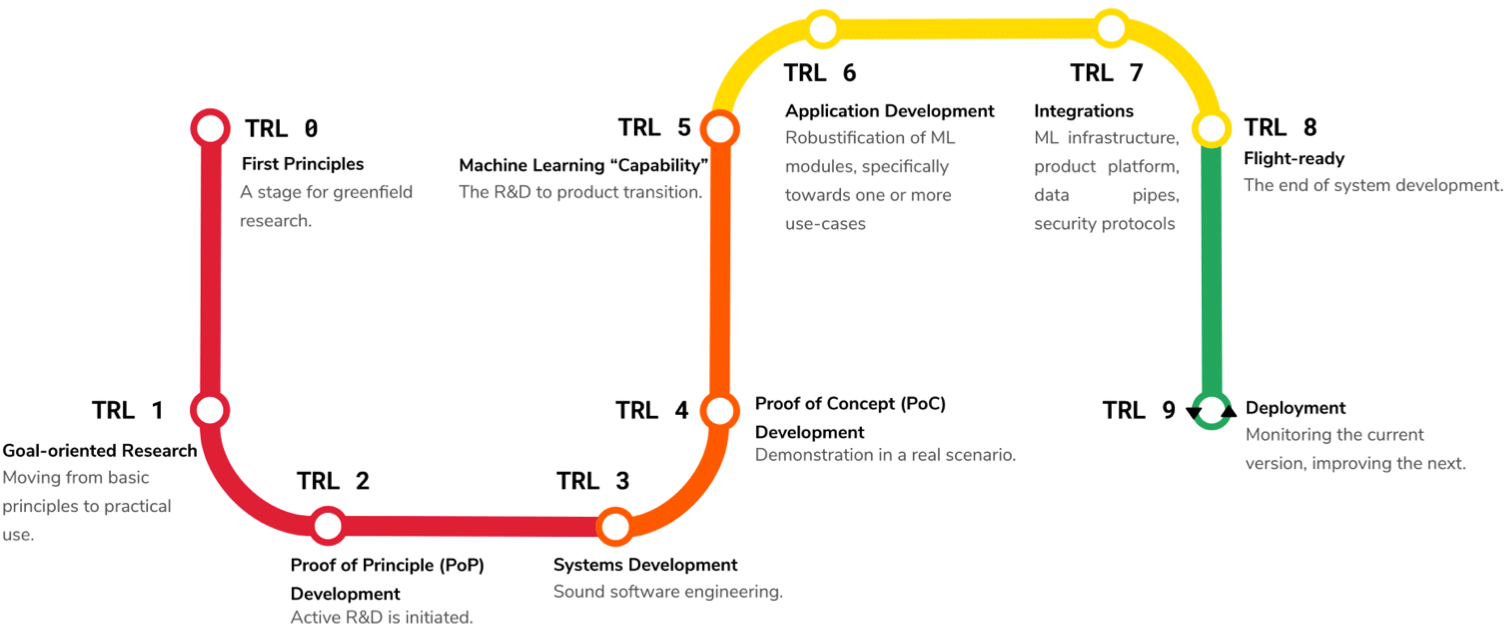
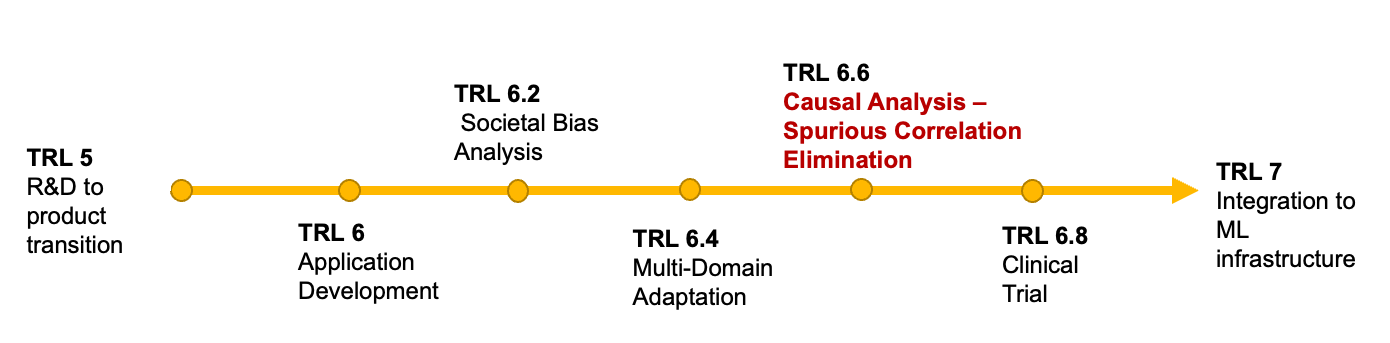
Medical imaging is an umbrella term encompassing a number of imaging techniques including Magnetic Resonance Imaging (MRI), X-ray imaging, Computed Tomography (CT), and Ultrasound (US) imaging , and is used primarily as supporting tool for diagnosis and monitoring of diseases. From a computational perspective, the community has engaged in a wide variety of tasks concerning the automated interpretation of medical imaging and enabling a range of applications. Machine learning (ML) shows significant successes for applications like automated localization and delineation of lesions and anatomies (Ronneberger et al., 2015; Kamnitsas et al., 2017) as well as for the automated alignment of scans between patients and mapping of patient anatomy into canonical interpretation spaces (Maintz and Viergever, 1998; Haskins et al., 2020; Grzech et al., 2020; Cabezas et al., 2011). Despite good in silico results, many of the approaches fail to translate into the clinical practice. While the reasons behind this can be complex and diverse, many have as a common factor the inability to adapt and be robust in clinical practice. Mapping this to the popular systems engineering framework of Technology Readiness Levels (TRL) (Lavin et al., 2021) as shown in Figure 1, medical imaging AI/ML applications often skip from TRL 4 – proof of concept– to TRL 7 –deployment– overlooking the very important TRLs 5 and 6 that make new systems robust to real world conditions. In Figure 2 we exhibit a finer grain view on the steps between TRL 6 and 7 that we deem to be important during the development of production-level medical imaging ML algorithms.

Refer to caption — Figure 1: Technology Readiness Levels of ML Systems - most applications skip levels 5,6 where algorithms are made robust and production ready. Figure reproduced from source without alterations; Source: (Lavin et al., 2021)

Concerning is the inability of commonly used AI/ML medical imaging methods to differentiate between correlations and causation, making potentially deadly mistakes in the process. For example, (DeGrave et al., 2021) identified a number of approaches that claim to have been able to diagnose COVID-19 from chest X-rays but ultimately fail to do so as they were instead picking up spurious correlations like hospital identifiers and the ethnicity of the patient.

As pointed out by (Castro et al., 2020a; Prosperi et al., 2020), ML for medical imaging is susceptible to different domain shifts that affect algorithmic performance and robustness in new environments. Population shifts occur when the train and test populations exhibit different characteristics that might include the prevalence of diseases, for example prevalence of lung nodules in polluted urban environments is higher than in a rural setting. An ML model trained in one of the two settings is not able to condition on the true causal links that are unseen in the images, hence, treats both populations the same way.

Acquisition and annotation shifts effect the production of both images and ground truth labels used to train ML algorithms. For example the same MRI scanner used to acquire both images and annotations can lead to two different datasets, dependent on the scanner settings and medical beliefs of the radiologist performing the annotations.

Finally, data selection biases are especially prevalent in the medical domains where expanded datasets can be hard to create for ethical, economic, and legal reasons.

If acknowledged and mitigated by causal analysis, the aforementioned biases can help build robust and adaptable ML algorithms for medical imaging that minimize the chances of dangerous predictions due to spurious correlations. In essence, many of the negative phenomena seen in ML for medical imaging could be solved if the community expands its involvement with the TRL points shown in Figure 2, which suggest the inclusion of causal analysis as an important step. However, causal analysis is not commonly used for the development of ML applications for medical imaging. Thus, in this review we explore recent research in this direction and the use of causal analysis for medical image machine learning applications. We looked at the major conferences - from example MICCAI, ISBI, IPMI from 2018 to April 2022- and journals of our field as well as some seminal preprints and included all that were directly related to both machine learning for medical imaging and causal reasoning. For a work to classify in our view, mentions of causality should transcend the discussion phase and be explicitly involved in the development or operation of the methods. In addition we will attempt to identify trends and lay out our beliefs for future directions of this field.

Throughout the following survey we assume that the reader is familiar with the notions of machine learning for medical imaging. While we invite the reader to refer to (Pearl, 2009) for an in depth textbook of causality and (Yao et al., 2021; Sanchez et al., 2022b) for a survey in the general state of the art in causal ML and an opinion piece on the use of causality in medical machine learning respectively. We are attaching a small description and discussion of the key concepts related to this survey.

2 Background

We first introduce key concepts required for the upcoming discussion of causality-driven methods in medical image analysis. In Section 2.1 we are discussing the concepts of Structural Causal Models (SCM) and their parametrization as Directed Acyclical Graphs (DAG) as introduced by J. Pearl (Pearl, 2009). In Section 2.2 we are defining the notions behind Rubin’s Potential Outcomes framework.

2.1 Structural causal models

Definition 1 (Structural Causal Model)

A structural causal model (SCM) specifies a set of latent variables $U=\{u_{1},\dots,u_{m}\}$ distributed as $P(U)$ , a set of observable variables $=\{v_{1},\dots,v_{n}\}$ , a directed acyclic graph (DAG), called the causal structure of the model, whose nodes are the variables $U\cup V$ , a collection of functions $F=\{f_{1},\dots,f_{n}\}$ , such that $v_{i}=f_{i}(PA_{i},u_{i}),\text{ for }i=1,\dots,n,$ where $PA$ denotes the parent observed nodes of an observed variable.

The collection of functions $F$ and the distribution over latent variables induces a distribution over observable variables: $P(V=v):=\sum_{\{u_{i}\mid f_{i}(PA_{i},u_{i})\,=\,v_{i}\}}\\ P(u_{i})$ In this manner, we can assign uncertainty over observable variables despite the fact the underlying dynamics are deterministic.

Moreover, the $do$ -operator forces variables to take certain values, regardless of the original causal mechanism. Graphically, $do(X=x)$ means deleting edges incoming to $X$ and setting $X=x$ . Probabilities involving $do(x)$ are normal probabilities in submodel $M_{x}$ : $P(Y=y\mid\text{do}(X=x))=P_{M_{x}}(y)$ .

Counterfactual inference The latent distribution $P(U)$ allows one to define probabilities of counterfactual queries, $P(Y_{y}=y)=\sum_{u\mid Y_{x}(u)=y}P(u).$ For $x\neq x^{\prime}$ one can also define joint counterfactual probabilities, $P(Y_{x}=y,Y_{x^{\prime}}=y^{\prime})=\sum_{u\mid Y_{x}(u)=y,\text{ }\&Y_{x^{\prime}}(u)=y^{\prime}}P(u).$ Moreover, one can define a counterfactual distribution given seemingly contradictory evidence. Given a set of observed evidence variables $E$ , consider the probability $P(Y_{{x}}={y}^{\prime}\mid E={e})$ .

Definition 2 (Counterfactual)

The counterfactual sentence “ $Y$ would be $y$ (in situation $U=u$ ), had $X$ been $x$ ”, denoted $Y_{x}(u)=y$ , corresponds to $Y=y$ in submodel $M_{x}$ for $U=u$ .

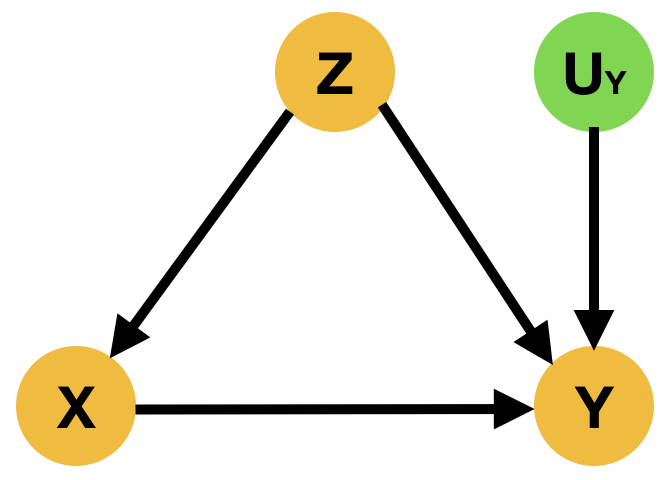
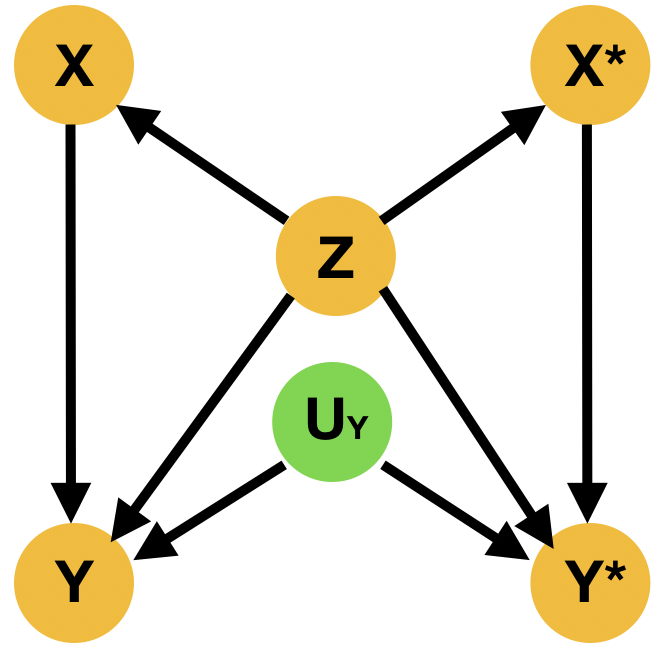
Despite the fact that this query may involve interventions that contradict the evidence, it is well-defined, as the intervention specifies a new submodel. Indeed, $P(Y_{x}={y}^{\prime}\mid E={e})$ is given by (Pearl, 2009) $\sum_{{u}}P(Y_{{x}}({u})={y}^{\prime})P({u}|{e})\,.$ There are two main ways to resolve this type of questions; the Abduction-Action-Prediction paradigm and the Twin Network paradigm shown respectively in ML literature among others in (Castro et al., 2020b; Vlontzos et al., 2021a). In short given SCM $M$ with latent distribution $P(U)$ and evidence ${e}$ , the conditional probability $P(Y_{{x}}\mid{e})$ is evaluated as follows: 1) Abduction: Infer the posterior of the latent variables with evidence ${e}$ to obtain $P(U\mid{e})$ , 2) Action: Apply $\text{do}({x})$ to obtain submodel $M_{x}$ , 3) Prediction: Compute the probability of $Y$ in the submodel $M_{x}$ with $P(U\mid{e})$ . Meanwhile the Twin Network paradigm casts the resolution of counterfactual queries to Bayesian feed-forward inference by extending the SCM to represent both factual and counterfactual worlds at once (Balke and Pearl, 1994). We exhibit an illustration of the twin network paradigm in Figure 3

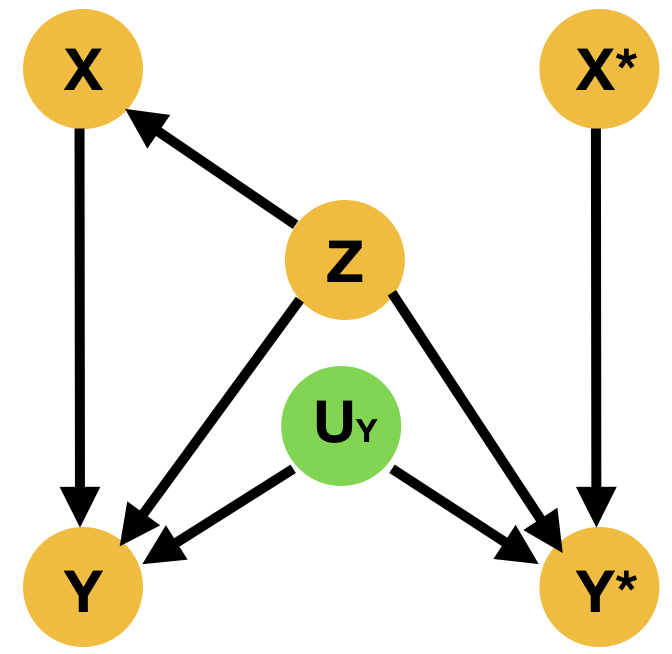
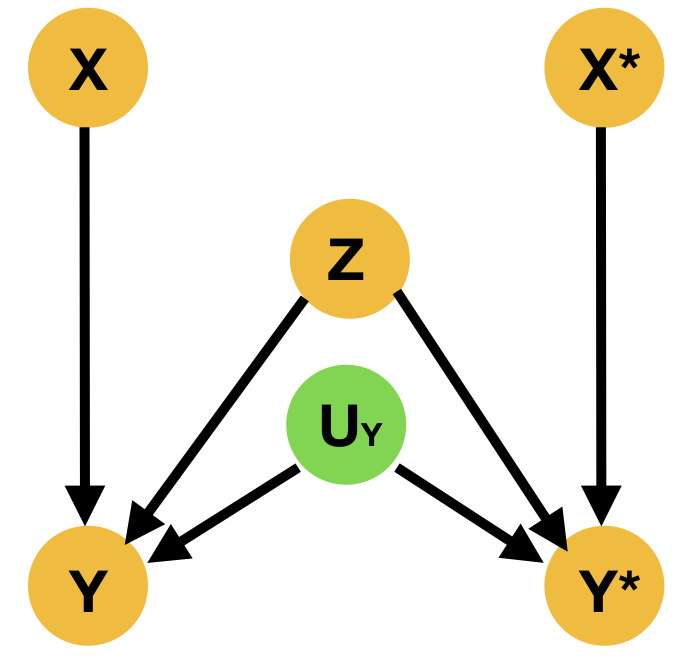
2.2 Potential outcomes – Average treatment effect

The potential outcomes framework introduced by (Splawa-Neyman et al., 1990) and (Rubin, 1978) explore the potential outcomes of a given intervention. Formally the framework is primarily interested in $Y(a),a\in\mathcal{C}$ where $Y$ is the outcome given intervention $a$ which belongs in the set of possible actions $\mathcal{C}$ . For the simple case where we are interested in the outcome of a specific treatment, we can use the following definitions:

Definition 3 (Treatment under Potential Outcomes)

$\mathcal{D}_{i}$ : Indicator of treatment intake for unit $i$

\mathcal{D}_{i}=\begin{cases}1,&\text{if unit $i$ received the treatment }\\ 0,&\text{otherwise}\end{cases}

(1)

Definition 4 (Potential Outcomes)

$\mathcal{Y}_{di}$ : Potential outcomes for unit $i$ depending if treatment has been applied or not

\mathcal{Y}_{di}=\begin{cases}\mathcal{Y}_{1,i},&\text{Potential Outcome for unit $i$ receiving the treatment }\\ \mathcal{Y}_{0,i},&\text{Potential Outcome for unit $i$ not receiving the treatment }\end{cases}

(2)

Using these quantities we are able to define the causal effect

Definition 5 (Causal Effect)

Causal Effect of the treatment on the outcome for unit $i$ is the difference between its two potential outcomes:

\tau_{i}=\mathcal{Y}_{1,i}-\mathcal{Y}_{0,i}

(3)

In Equation 3 we define the causal treatment effect for an individual unit $i$ . We can also define the average treatment effect that looks into a group of individual units $i\in\mathcal{G}$ .

Definition 6 (Average Treatment Effect)

$\tau_{ATE}$ is the difference between all treatment potential outcomes and all control potential outcomes

\begin{split}\tau_{ATE}&=\frac{1}{N}\sum^{N}_{i}\mathcal{Y}_{1,i}-\frac{1}{N}\sum^{N}_{i}\mathcal{Y}_{0,i}\\ &=E[\mathcal{Y}_{1,i}-\mathcal{Y}_{0,i}]\\ &=E[\tau_{i}]\end{split}

(4)

In literature we can find many variation of this measure like the individual treatment effect (eg. (Mueller et al., 2021)) where we look on the treatment effect on an individual rather than aggregate over a population. In the interest of conciseness we will not be be exploring the full range of possible variations upon the ATE in this survey but just acknowledge that they exist and call upon them depending on the method we are discussing.

One last concept required for our discussion is propensity score. Introduced by (Rosenbaum and Rubin, 1983) it is defined to be the probability of treatment assignment conditioned on observed covariates. Mathematically it can be described as $e=P(T\mid X)$ where $X$ are the covariates and $T$ the treatment. Commonly used as a matching criterion to form sets of treated and untreated subjects that are close in the covariate space; these sets are subsequently used to estimate the causal effect of the treatment.

3 Causal discovery in medical imaging

Causal discovery is an open and challenging research problem, directly touching the most fundamental aspects of scientific exploration; the discovery of causal relations (Vowels et al., 2021). In this setting we are trying to estimate the mechanisms that describe the causal links between variables from data. In order to make the problem of causal discovery tractable, common causal discovery methods make a series of assumptions that can be summarized as:

•
Acyclicity: we are able to describe the causal structure as a Directed Acyclical Graph (DAG)
•
Markovian: all nodes are independent of their non-descendant when conditioned on their parents
•
Faithfulness: all conditional independences are represented in the DAG
•
Sufficiency: any pair of nodes in the DAG have no common external causes

Moreover, the vast majority of approaches tackling causal discovery formulate the problem as graph modeling challenge. We refer the reader to (Glymour et al., 2019; Vowels et al., 2021) for a more thorough review of causal discovery methods based on graphical models. For the purposes of this survey we note that methods are often categorized based on their approach into constraint-based, score-based and optimization-based Zheng et al. (2018) methods.

Constraint-based methods relate to approaches like (Spirtes et al., 2000) PC and Fast Causal Inference (FCI) that test conditional independence between factors to assess their causal links. The main intuition is that two statistically independent variables are not causally linked. First, pairwise independence is evaluate to determine the undirected structure. Following this conditional independence is tested to orient the links between the nodes. If two nodes fail this test, then they can be added to the separation set of each other used to orient colliders - nodes of the causal graph with two or more incoming links. The main difference between the aforementioned PC and FCI algorithms is FCI’s ability to be asymptotically correct in the presence of confounders. Both of them are however limited to the causal equivalence classes, i.e., causal structures that satisfy the same conditional Independence. A method that searches over the space of possible equivalence classes is the Greedy Equivalence Search (GES) (Chickering, 2003) officially considered a score-based method which uses the Bayesian Information Criterion (BIC). Similarly, Pamfil et al. (2020) use a score based approach that characterizes the acyclicity constraint of Directed Acyclical Graphs as a smooth equality constraint.

In the computer vision field, visual causal discovery has been spearheaded by tasks related to the CLEVRER dataset (Yi et al., 2020) where ML algorithms are asked to understand a video scene and answer counterfactual questions.(Li et al., 2020) learn to predict causal links from videos, by parameterizing the causal links as strings and springs where the algorithm predicts their parameters. (Löwe et al., 2022) perform a similar task by inferring stationary causal graphs from videos. Furthermore, (Nauta et al., 2019) develop a causal discovery method based upon the use of attention-enabled convolutional neural networks. (Ke et al., 2022) address the task of causal discovery by training a neural network to induce causal dependencies by predicting causal adjacency matrices between variables. Finally, works like (Gerstenberg et al., 2021) analyze how humans perform the task of causal discovery in relation to how machine learning approaches the same task.

In the sub-field of medical imaging, causal discovery has not been explored to its fullest potential. Most works involve functional Magnetic Resonance Imaging (f-MRI). f-MRI is able to highlight active areas of the brain, and as during different physiological processes (working or resting) activate a series of brain areas. Causal discovery in f-MRI attempts to identify causal links among neural processes. (Sanchez-Romero et al., 2018, 2019) diverge from the usual DAG paradigm and introduce the Fast Adjacency Skewness (FASK) method which exploits non-Gaussian features of blood-oxygen-level-dependent (BOLD) signals to identify causal feedback mechanisms. In a very interesting work, (Huang et al., 2020) parametrize both causal discovery in f-MRI and domain adaptation as a non-stationary causal task that they then proceed to solve. In the field of medicine but not imaging (Mani and Cooper, 2000) extract causal relations from medical textual data.

(Bielczyk et al., 2017) looked into applications on f-MRI and extracting causal relations between neural processes by applying the most common causal inference techniques including dynamic causal modeling, Bayesian networks, transfer entropy and ranked them based on their perceived suitability and performance on the tasks at hand. Similarly, (Cortes-Briones et al., 2021) explore deep learning methods for schizophrenia analysis and outcome prediction, mostly with the use of f-MRI inputs, and argue for the need of causally enabled ML methods to produce plausible hypothesis explaining observed phenomena. Recently (Chuang et al., 2022) propose deep stacking networks (DSNs), with adaptive convolutional kernels (ACKs) as component parts to aid the identification of non-linear causal relationships.

Furthermore, (Jiao et al., 2018) discuss bivariate causal discovery for imaging data. The authors develop a non-linear additive noise model for that they show a causal discovery task with genetic data and for causal inference in the Alzheimer’s Disease Neuroimaging Initiative (ADNI) MRI data. (Reinhold et al., 2021) propose a Structural causal model that encodes causal functional relationships between demographics and disease covariates with MRI images of the brain in an attempt to identify Multiple Sclerosis (MS).

While the field of medicine is governed by causal relations between physiological processes, little work has been done in the field of medical imaging and causal discovery. We believe that this is mostly due to the significant inherent difficulty of the task at hand, in conjunction with the lack of the required meta-data that are needed to characterize causal links that are not visible in the image. In other words, we do not think that images by themselves possess enough information for identification of causal links but we are adamant that they can serve as a useful tool and source of extra information when combined with medical knowledge. It is, however, important to note the potential the aforementioned time-series based causal discovery methods exhibit as f-MRIs can themselves be thought of as time-modulated events, and be used in conjunction with other time-based modalities.

Finally, relating back to Figure 2, causal discovery can aid bring to light causal links that were not previously known. It can further help, probe the beliefs of other algorithms and hence root out spurious correlations or the encoding of societal biases that their creators carried. As such we believe that causal discovery can assist the completion of TRLs 6.6 through audits of the practitioners beliefs. Most importantly, however, in the subsequent sections we will be discussing causal inference, that assumes the existence of high quality causal diagrams. Causal discovery is responsible for establishing these diagrams and hence indirectly contributing significantly at TRLs 6-6.4.

4 Causal Inference in medical imaging

While causal discovery using medical images is limited to some applications involving f-MRI scans, causal inference is significantly more active as an area of research. Highlighting its importance, (Castro et al., 2020a) argue that causal inference can be used to alleviate some of the most prominent problems in medical imaging. They argue that acquisition and annotation of medical images can exhibit bias from the annotators and curators of the datasets. As such, causality aware methods can learn to account for such biases and reduce their effects. Moreover, as the training datasets represent a limited population with specific characteristics, medical imaging algorithms are susceptible to population, selection and prevalence biases if not properly controlled for these variations. These biases could for example arise when an algorithm is trained by a vast majority on data that come from a given geographical region $X$ , then it implicitly learns the prevalence of diseases for that group; if it is deployed in a different region with a population that is characterized by different genotype and phenotype characteristics, the biases that the algorithm has learned could lead to mis- or under- diagnosis of diseases.

In our exploration of the use of causal inference in medical imaging literature we identified five main sub-fields of research that leverage causal insights. We found that causal inference is overwhelmingly used to contribute to fairness, safety and explainability of the existing approaches. There are some albeit limited uses in generative modeling of medical images, domain generalization and out-of-distribution detection. As we will expand in the following sections, we believe these areas are ready for more applications of causal inference.

We note that all the works mentioned below have causality as a key part of their proposed methodologies. We extended our survey not only to peer reviewed publications but also to notable preprints that appear to have produced significant discussion in the machine learning medical imaging community.

4.1 Medical Analysis

We continue our survey with causally enabled methods for medical analysis that utilize imaging data.

In (Wang et al., 2021) the authors use a normalizing flow-based causal model similar to (Pawlowski et al., 2020) in order to harmonize heterogeneous medical data. Applied to T1 brain MRI for the classification of Alzheimer’s disease, the method abides by the abduction-action-prediction paradigm to infer counterfactuals which are then used to harmonize the medical data. (Pölsterl and Wachinger, 2021) circumvent the identifiability condition that all confounders have to be known and measured by leveraging the dependencies between causes in order to determine substitute confounders; they apply their method in brain neuroimaging for Alzheimer’s disease detection. On a similar note, (Zhuang et al., 2021) issue an alternative to expectation maximization(EM) for dynamic causal modeling in f-MRI brain scans. Their approach is based upon the multiple-shooting method to estimate the parameters of ordinary differential equations (ODEs) under noisy observations required for brain causal modeling. The authors suggest an augmentation of the aforementioned method called multiple-shooting adjoint method by using the adjoint method to calculate the loss and gradients of their model.

(Clivio et al., 2022) propose a neural score matching method for high dimensional data that could be potentially very helpful for the development of medical imaging applications as they develop methods for causal inference in high dimensional settings; allowing thus the use of medical images in a more straightforward way that avoids pre-processing them to a lower dimensional latent space. Finally, (Ramsey et al., 2010) identified six problems that causal inference can assist in solving in the field of functional MRI analysis.

4.2 Fairness, Safety & Explainability

Another application of causal inference in the field of medical imaging revolves around fairness, safety and explainability, directly related to TRLs 6.2 6.6 and 6.8. Medical tools like medical imaging analysis have a significant impact on the well-being of people affected by their use. Doctors and patients alike need to be able to trust the AI/ML methods in order to use them, while contrary to other AI/ML applications unwanted bias and poor performance can often be deadly. As such, the need to have fair, safe and explainable algorithms arises. Causal inference is a great tool to analyze black box AI/ML methods and make sure that they are not carrying unwanted societal biases and mitigate any robustness problems that might arise.

In this field (Kayser et al., 2020) accompany their ML algorithm to detect polyps in human intestines with a causality inspired analysis on the effectiveness of their method. Similarly (da Silva et al., 2020) use generative model produced brain MRI images of brain atrophy to evaluate and explore different causal hypothesis on brain growth and atrophy. On a similar note (Li et al., 2021) develop a causal inference-based method to search associations in genomics data from the UK Biobank. Additionally, (Baniasadi et al., 2022) employ causal analysis to explain the performance of their brain structure segmentation network. Similarly (Singla et al., 2021) employ mediation analysis to identify the units and parameters of radiological reports that influence their classifier’s outcomes; this method is applied on chest X-rays. In their work (Zapaishchykova et al., 2021) develop a Bayesian causal model to interpret the outputs and functionality of their Faster-RCNN based pelvic fracture classifier in CT images. Their Bayesian causal model matches lower confidence predictions with higher confidence ones and then updates the prediction set based on these matching. (Garcia Santa Cruz et al., ) explore the effect of uncontrolled confounders in medical imaging applications and observe that regardless of task and architecture, total confounding can be used to explain the difference in performance between development of the models and real life applications. (Adebayo et al., 2022) evaluate new metrics to quantify the effect of spurious correlations in age regression from hand X-rays. They show that only under certain conditions these metrics can be trusted and call for a paradigm shift in the effort to identify spurious correlations

Concerning fairness, (Chen et al., 2021) discuss the effects of biases in medical ML and how biases like image acquisition, genetic variation, and intra-observer labeling result in healthcare disparities. They go on to argue that causal analysis in medical ML can greatly help mitigate such biases. Expanding on this argumentation, (Holzinger et al., 2022) argue that information fusion is key to achieve greater transparency and safety in medical imaging ML applications. In a slightly different position paper, (Santa Cruz et al., 2021) argue for the standardization of medical metadata in order to assist causal inference techniques in biomedical ML. Along similar lines, (Garcea et al., 2021) argues for the use of causal intuition when designing medical imaging datasets. Meanwhile, (Vlontzos et al., 2022) uses causal inference to estimate the necessity and sufficiency of the type and quantity of data to include in a medical imaging dataset in order to improve model performance under strict computational and financial constraints. In addition, (Vlontzos et al., 2021b) contend that causal analysis can help alleviate biases and provide the necessary trust to medical imaging application in deep space manned missions.

Finally, (Bernhardt et al., 2022) investigated questions of algorithmic fairness in medical imaging ML under a causal prism, focusing on the issue of under-diagnosis they highlighted some issues that warrant more attention in prior pieces of literature. (Schrouff et al., 2022) perform a thorough evaluation of the biases and unfairness that can arise in cross-hospital deployment of medical ML solutions asserting a causal analysis as a potential method to alleviate these issues. (Benkarim et al., 2021) use propensity scores (see section 2.2) to quantify diversity due to major sources of population stratification and hence assess fairness.

4.3 Generative methods

Generative modeling attempts to learn variable interdependencies such that the model is able to generate realistic samples that abide by certain characteristics aiding the admittance past TRLs 6.4 and 6.8. Variational Autoencoders (Kingma and Welling, 2013), Generative adversarial networks (Goodfellow et al., 2014) and normalizing flows (Dinh et al., 2017) are examples for approaches that try to estimate the underlying data distribution from which they then sample to produce new data. Causal inference in generative modeling is a relatively underdeveloped field, especially in the context of medical imaging due to the inherit difficulty to acquire good quality training signals for the counterfactual samples.

(Gordaliza et al., 2022) develop a two stage methodology where Tuberculosis infected lung CT images are analyzed in a disentangled manner and produce counterfactual images depicting how the patient would look like if they were healthy. Contrary to other approaches the authors use a DAG to represent the image generation process and parametrize it using a neural network such that sampling and use of it is straightforward for the counterfactual generation step. (Pawlowski et al., 2020) developed a normalizing flow model to perform the abduction step in an abduction-action-prediction counterfactual inference task and are able to generate plausible brain MRI volumes. Reynaud et al. in (Reynaud et al., 2022) assume a different approach and develop a generative model based on Deep Twin Networks (Vlontzos et al., 2021a). Performing counterfactual inference in the latent space embeddings, the authors are able to generate realistic Ultrasound Videos with different Left Ventricle Ejection Fractions. Their approach is similar to (Kocaoglu et al., 2018) in the sense that a GAN is used to provide a training signal for the generated, counterfactual samples. Moreover, (Kumar et al., 2022) in a methodologically similar note, generate counterfactual images to guide the discovery of medical biomarkers in brain MRI volumes.

Finally (Sanchez et al., 2022a) use deep diffusion model to ask counterfactual questions and generate hard to obtain medical scans. These, in turn, are used to augment existing datasets for other downstream tasks.

4.4 Domain Generalization

One of the most promising areas where causal reasoning can be applied in the field of medical imaging is Domain Adaptation and Out-of-Distribution detection, directly associated with TRL 6.4. If we model the generative process that results in a medical image and include factors like the medical history, the disease, imaging domain, etc. we can then go on and interpret domain generalization and adaptation as a model that is able to perform well under different treatments in the imaging domain parameter, as argued by (Huang et al., 2020). In their paper Huang et al model domain adaptation as a non stationary change in the underlying causal graph and propose methods to identify and resolve these changes. (Zhang et al., 2021) analyze the domain shifts experienced in clinical deployment of AIML algorithms from a causal perspective and then proceed to investigate and benchmark eight popular methods of domain generalization. They find that domain generalization methods fail to provide any improvement in performance over empirical risk minimization in situations where we find sampling bias. Similarly (Fehr et al., 2022) model the causal relationships leading to the medical images and create synthetic datasets in order to evaluate the transportability of methods to external settings where interventions on factors like ages, sex and medical metrics have been performed.

(Ouyang et al., 2021) apply a causal analysis on the problem of domain generalization in segmentation of medical images. They first simulate shifted domain images via a randomly weighted shallow network; then they intervene upon the images such that spurious correlations are removed and finally train their segmentation model while enforcing a domain invariance condition. (Valvano et al., 2021) develop a method to reuse adversarial mask discriminators for test-time training to combat distribution shifts in medical image segmentation tasks. In their discussion of their method they explain the good performance of their method under a causal lens. Finally (Kouw et al., 2019) build a causal Bayesian prior to aide MRI tissue segmentation to generalize across different medical centers.

4.5 Out of Distribution Robustness & Detection

We ought to consider the use of causal reasoning and inference on out of distribution detection tasks aiding TRLs 6.6 and 6.8. Commonly seen as anomaly detection tasks many methodologies attempt to learn the underlying distribution of “normal”- in-distribution data and assess whether test out-of-distribution “pathological” samples belong to the same distribution or not. In a related task, researchers sometimes treat the out-of-distribution as a robustness criterion and attempt to develop methodologies that can operate equally well in all domains. It is evident that an alternative, where we learn the causal dependencies that make samples that are considered out-of-distribution can yield significant benefits in the field of anomaly detection. In this sub-field we only found a few works exploring this approach in medical imaging but we believe that more works will appear once the community gets more familiar with the benefits of causal reasoning.

(Ye et al., 2021b) give a causal explanation to diversity and correlation shifts and proceed to benchmark out-of-distribution methods, showing that the aforementioned shifts are the main components of the distribution shifts found in OOD datasets. Similarly (Ye et al., 2021a), introduce an influence function and a novel metric to evaluate OOD while analyzing their contributions from a causal standpoint. (Liu et al., 2021) propose a causal semantic generative model in order to address OOD prediction from a single training domain. Utilizing the causal invariance principle they disentangle the semantic causes of prediction and other variation factors achieving impressive results.

On the robustness of medical procedures (Ding et al., 2022), built a causal tool segmentation model that iteratively aligns tool masks with observations. Unable to deal with occlusions and without leveraging temporal information the authors of this recent work also comment on the future next steps of robust causal machine learning tools.

Even though not directly applied in medical imaging, causality has been playing an important role in the algorithmic robustness literature as seen in (Zhang et al., 2022; Papangelou et al., 2018). Meanwhile the machine learning for medical imaging community has shown great interest in developing robust algorithms, (Hirano et al., 2021; Huang et al., 2019). We hope that these two communities will soon come together and use causal reasoning in making machine learning for medical imaging algorithms robust.

5 Discussion and Conclusion

We have identified a wide range of possible applications of causality in medical imaging. However, we have not yet observed an enthusiastic uptake of causal reasoning and causal considerations from the community. We believe that introducing causal reasoning in medical imaging applications would benefit both the performance and robustness of the algorithms but most of all would provide the required scrutiny and security that doctors demand from their tools. A model that is able to be probed causally and does not operate as a black box can be trusted more easily by healthcare professionals since they will be able to understand its inner workings; enabling safe human-machine decision making (Budd et al., 2021). Moreover it would ameliorate the legal hurdle of accountability that developers of medical ML applications face, as we would be able to explain the processes and logic of the models. As machine learning algorithms in medical imaging make their way towards clinical practice we hope to see more causal machine learning solutions being trialed.

Furthermore, as medical and medical imaging applications move away from large hospitals, towards first responders, remote community doctors and even astronauts, we need tools that are robust to extreme circumstance differences. Causally enabled ML has shown great promise in its ability to adapt as it does not depend on correlations that might or might not exist in the new domain, but, like humans, it taps into the underlying causal relationships that are very hard to shift. That being said, causal ML is not a panacea; our theoretical capabilities restrict absolute certainty to a limited number of well defined conditions that Causal Diagrams have to obey. When shifting focus to real life scenarios, we are forced to accept trade offs and be considerate about the limitations of our approaches.

Causally enabled ML for medical imaging is a very promising research field that the authors of this survey believe is vital for next generation of tools for medical imaging. We are very excited about what the future of this research might bring and we hope to have inspired researchers and practitioners with this review to consider the causal ML route for medical imaging research and application development.

References

Adebayo et al. (2022) J. Adebayo, M. Muelly, H. Abelson, and B. Kim. Post hoc explanations may be ineffective for detecting unknown spurious correlation. In International Conference on Learning Representations, 2022. URL https://openreview.net/forum?id=xNOVfCCvDpM.
Balke and Pearl (1994) A. Balke and J. Pearl. Probabilistic evaluation of counterfactual queries. In AAAI, 1994.
Baniasadi et al. (2022) M. Baniasadi, M. V. Petersen, J. Goncalves, A. Horn, V. Vlasov, F. Hertel, and A. Husch. Dbsegment: Fast and robust segmentation of deep brain structures–evaluation of transportability across acquisition domains. Human Brain Mapping, 2022.
Benkarim et al. (2021) O. Benkarim, C. Paquola, B.-y. Park, V. Kebets, S.-J. Hong, R. V. de Wael, S. Zhang, B. T. Yeo, M. Eickenberg, T. Ge, et al. The cost of untracked diversity in brain-imaging prediction. bioRxiv, 2021.
Bernhardt et al. (2022) M. Bernhardt, C. Jones, and B. Glocker. Investigating underdiagnosis of ai algorithms in the presence of multiple sources of dataset bias. arXiv preprint arXiv:2201.07856, 2022.
Bielczyk et al. (2017) N. Z. Bielczyk, S. Uithol, T. van Mourik, M. N. Havenith, P. Anderson, J. C. Glennon, and K. Buitelaar. Causal inference in functional magnetic resonance imaging. arXiv preprint arXiv:1708.04020, 2017.
Budd et al. (2021) S. Budd, E. C. Robinson, and B. Kainz. A survey on active learning and human-in-the-loop deep learning for medical image analysis. Medical Image Analysis, 71:102062, 2021. ISSN 1361-8415.
Cabezas et al. (2011) M. Cabezas, A. Oliver, X. Lladó, J. Freixenet, and M. B. Cuadra. A review of atlas-based segmentation for magnetic resonance brain images. Computer methods and programs in biomedicine, 104(3):e158–e177, 2011.
Castro et al. (2020a) D. C. Castro, I. Walker, and B. Glocker. Causality matters in medical imaging. Nature Communications, 11(1):3673, Jul 2020a.
Castro et al. (2020b) D. C. Castro, I. Walker, and B. Glocker. Causality matters in medical imaging. Nature Communications, 11(1):1–10, 2020b.
Chen et al. (2021) R. J. Chen, T. Y. Chen, J. Lipkova, J. J. Wang, D. F. Williamson, M. Y. Lu, S. Sahai, and F. Mahmood. Algorithm fairness in ai for medicine and healthcare. arXiv preprint arXiv:2110.00603, 2021.
Chickering (2003) D. M. Chickering. Optimal structure identification with greedy search. J. Mach. Learn. Res., 3(null):507–554, mar 2003. ISSN 1532-4435.
Chuang et al. (2022) K.-C. Chuang, S. Ramakrishnapillai, L. Bazzano, and O. Carmichael. Nonlinear conditional time-varying granger causality of task fmri via deep stacking networks and adaptive convolutional kernels. In L. Wang, Q. Dou, P. T. Fletcher, S. Speidel, and S. Li, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2022, pages 271–281, Cham, 2022. Springer Nature Switzerland.
Clivio et al. (2022) O. Clivio, F. Falck, B. Lehmann, G. Deligiannidis, and C. Holmes. Neural score matching for high-dimensional causal inference. AISTATS, 2022.
Cortes-Briones et al. (2021) J. A. Cortes-Briones, N. I. Tapia-Rivas, D. C. D’Souza, and P. A. Estevez. Going deep into schizophrenia with artificial intelligence. Schizophrenia Research, 2021.
da Silva et al. (2020) M. da Silva, K. Garcia, C. H. Sudre, C. Bass, M. J. Cardoso, and E. Robinson. Biomechanical modelling of brain atrophy through deep learning. arXiv preprint arXiv:2012.07596, 2020.
DeGrave et al. (2021) A. J. DeGrave, J. D. Janizek, and S.-I. Lee. Ai for radiographic covid-19 detection selects shortcuts over signal. Nature Machine Intelligence, 2021.
Ding et al. (2022) H. Ding, J. Zhang, P. Kazanzides, J. Y. Wu, and M. Unberath. Carts: Causality-driven robot tool segmentation from vision and kinematics data. In L. Wang, Q. Dou, P. T. Fletcher, S. Speidel, and S. Li, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2022, pages 387–398, Cham, 2022. Springer Nature Switzerland.
Dinh et al. (2017) L. Dinh, J. Sohl-Dickstein, and S. Bengio. Density estimation using real nvp. ICLR, 2017.
Fehr et al. (2022) J. Fehr, M. Piccininni, T. Kurth, and S. Konigorski. A causal framework for assessing the transportability of clinical prediction models. medRxiv, 2022.
Garcea et al. (2021) F. Garcea, L. Morra, and F. Lamberti. On the use of causal models to build better datasets. In 2021 IEEE 45th Annual Computers, Software, and Applications Conference (COMPSAC), pages 1514–1519. IEEE, 2021.
(22) B. Garcia Santa Cruz, A. Husch, and F. Hertel. The effect of dataset confounding on predictions of deep neural networks for medical imaging.
Gerstenberg et al. (2021) T. Gerstenberg, N. D. Goodman, D. A. Lagnado, and J. B. Tenenbaum. A counterfactual simulation model of causal judgments for physical events. Psychological review, 128(5):936, 2021.
Glymour et al. (2019) C. Glymour, K. Zhang, and P. Spirtes. Review of causal discovery methods based on graphical models. Frontiers in Genetics, 10, 2019. ISSN 1664-8021. doi: 10.3389/fgene.2019.00524. URL https://www.frontiersin.org/article/10.3389/fgene.2019.00524.
Goodfellow et al. (2014) I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio. Generative adversarial nets. Advances in neural information processing systems, 27, 2014.
Gordaliza et al. (2022) P. M. Gordaliza, J. J. Vaquero, and A. Munoz-Barrutia. Translational lung imaging analysis through disentangled representations. arXiv preprint arXiv:2203.01668, 2022.
Grzech et al. (2020) D. Grzech, B. Kainz, B. Glocker, and L. Le Folgoc. Image registration via stochastic gradient markov chain monte carlo. In Uncertainty for Safe Utilization of Machine Learning in Medical Imaging, and Graphs in Biomedical Image Analysis, pages 3–12. Springer, 2020.
Haskins et al. (2020) G. Haskins, U. Kruger, and P. Yan. Deep learning in medical image registration: a survey. Machine Vision and Applications, 31(1):1–18, 2020.
Hirano et al. (2021) H. Hirano, A. Minagi, and K. Takemoto. Universal adversarial attacks on deep neural networks for medical image classification. BMC medical imaging, 21(1):1–13, 2021.
Holzinger et al. (2022) A. Holzinger, M. Dehmer, F. Emmert-Streib, R. Cucchiara, I. Augenstein, J. Del Ser, W. Samek, I. Jurisica, and N. Díaz-Rodríguez. Information fusion as an integrative cross-cutting enabler to achieve robust, explainable, and trustworthy medical artificial intelligence. Information Fusion, 79:263–278, 2022.
Huang et al. (2020) B. Huang, K. Zhang, J. Zhang, J. Ramsey, R. Sanchez-Romero, C. Glymour, and B. Schölkopf. Causal discovery from heterogeneous/nonstationary data with independent changes. JMLR, Jun 2020.
Huang et al. (2019) Y. Huang, T. Würfl, K. Breininger, L. Liu, G. Lauritsch, and A. Maier. Abstract: Some investigations on robustness of deep learning in limited angle tomography. In H. Handels, T. M. Deserno, A. Maier, K. H. Maier-Hein, C. Palm, and T. Tolxdorff, editors, MICCAI, pages 21–21, Wiesbaden, 2019. Springer Fachmedien Wiesbaden.
Jiao et al. (2018) R. Jiao, N. Lin, Z. Hu, D. A. Bennett, L. Jin, and M. Xiong. Bivariate causal discovery and its applications to gene expression and imaging data analysis. Frontiers in Genetics, 9, 2018. ISSN 1664-8021. doi: 10.3389/fgene.2018.00347. URL https://www.frontiersin.org/article/10.3389/fgene.2018.00347.
Kamnitsas et al. (2017) K. Kamnitsas, C. Ledig, V. F. Newcombe, J. P. Simpson, A. D. Kane, D. K. Menon, D. Rueckert, and B. Glocker. Efficient multi-scale 3D CNN with fully connected crf for accurate brain lesion segmentation. Medical image analysis, 36:61–78, 2017.
Kayser et al. (2020) M. Kayser, R. D. Soberanis-Mukul, A.-M. Zvereva, P. Klare, N. Navab, and S. Albarqouni. Understanding the effects of artifacts on automated polyp detection and incorporating that knowledge via learning without forgetting. arXiv preprint arXiv:2002.02883, 2020.
Ke et al. (2022) N. R. Ke, S. Chiappa, J. Wang, J. Bornschein, T. Weber, A. Goyal, M. Botvinic, M. Mozer, and D. J. Rezende. Learning to induce causal structure. 2022.
Kingma and Welling (2013) D. P. Kingma and M. Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
Kocaoglu et al. (2018) M. Kocaoglu, C. Snyder, A. G. Dimakis, and S. Vishwanath. Causalgan: Learning causal implicit generative models with adversarial training. In International Conference on Learning Representations, 2018.
Kouw et al. (2019) W. M. Kouw, S. N. Ørting, J. Petersen, K. S. Pedersen, and M. de Bruijne. A cross-center smoothness prior for variational bayesian brain tissue segmentation. In A. C. S. Chung, J. C. Gee, P. A. Yushkevich, and S. Bao, editors, Information Processing in Medical Imaging, pages 360–371, Cham, 2019. Springer International Publishing. ISBN 978-3-030-20351-1.
Kumar et al. (2022) A. Kumar, A. Hu, B. Nichyporuk, J.-P. R. Falet, D. L. Arnold, S. Tsaftaris, and T. Arbel. Counterfactual image synthesis for discovery of personalized predictive image markers. arXiv preprint arXiv:2208.02311, 2022.
Lavin et al. (2021) A. Lavin, C. M. Gilligan-Lee, A. Visnjic, S. Ganju, D. Newman, S. Ganguly, D. Lange, A. G. Baydin, A. Sharma, A. Gibson, et al. Technology readiness levels for machine learning systems. arXiv preprint arXiv:2101.03989, 2021.
Li et al. (2021) S. Li, M. Sesia, Y. Romano, E. Candès, and C. Sabatti. Searching for consistent associations with a multi-environment knockoff filter. arXiv preprint arXiv:2106.04118, 2021.
Li et al. (2020) Y. Li, A. Torralba, A. Anandkumar, D. Fox, and A. Garg. Causal discovery in physical systems from videos. Advances in Neural Information Processing Systems, 33:9180–9192, 2020.
Liu et al. (2021) C. Liu, X. Sun, J. Wang, H. Tang, T. Li, T. Qin, W. Chen, and T.-Y. Liu. Learning causal semantic representation for out-of-distribution prediction. Advances in Neural Information Processing Systems, 34, 2021.
Löwe et al. (2022) S. Löwe, D. Madras, R. Zemel, and M. Welling. Amortized causal discovery: Learning to infer causal graphs from time-series data, 2022.
Maintz and Viergever (1998) J. A. Maintz and M. A. Viergever. A survey of medical image registration. Medical image analysis, 2(1):1–36, 1998.
Mani and Cooper (2000) S. Mani and G. F. Cooper. Causal discovery from medical textual data. In Proceedings of the AMIA Symposium, page 542. American Medical Informatics Association, 2000.
Mueller et al. (2021) S. Mueller, A. Li, and J. Pearl. Causes of effects: Learning individual responses from population data. 2021.
Nauta et al. (2019) M. Nauta, D. Bucur, and C. Seifert. Causal discovery with attention-based convolutional neural networks. Machine Learning and Knowledge Extraction, 1(1):312–340, 2019.
Ouyang et al. (2021) C. Ouyang, C. Chen, S. Li, Z. Li, C. Qin, W. Bai, and D. Rueckert. Causality-inspired single-source domain generalization for medical image segmentation. arXiv preprint arXiv:2111.12525, 2021.
Pamfil et al. (2020) R. Pamfil, N. Sriwattanaworachai, S. Desai, P. Pilgerstorfer, K. Georgatzis, P. Beaumont, and B. Aragam. Dynotears: Structure learning from time-series data. In International Conference on Artificial Intelligence and Statistics, pages 1595–1605. PMLR, 2020.
Papangelou et al. (2018) K. Papangelou, K. Sechidis, J. Weatherall, and G. Brown. Toward an understanding of adversarial examples in clinical trials. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pages 35–51. Springer, 2018.
Pawlowski et al. (2020) N. Pawlowski, D. C. Castro, and B. Glocker. Deep structural causal models for tractable counterfactual inference. NeurIPS, 2020.
Pearl (2009) J. Pearl. Causality (2nd edition). Cambridge University Press, 2009.
Pölsterl and Wachinger (2021) S. Pölsterl and C. Wachinger. Estimation of causal effects in the presence of unobserved confounding in the alzheimer’s continuum. In A. Feragen, S. Sommer, J. Schnabel, and M. Nielsen, editors, Information Processing in Medical Imaging, pages 45–57, Cham, 2021. Springer International Publishing. ISBN 978-3-030-78191-0.
Prosperi et al. (2020) M. Prosperi, Y. Guo, M. Sperrin, J. S. Koopman, J. S. Min, X. He, S. Rich, M. Wang, I. E. Buchan, and J. Bian. Causal inference and counterfactual prediction in machine learning for actionable healthcare. Nature Machine Intelligence, 2(7):369–375, 2020.
Ramsey et al. (2010) J. D. Ramsey, S. J. Hanson, C. Hanson, Y. O. Halchenko, R. A. Poldrack, and C. Glymour. Six problems for causal inference from fmri. neuroimage, 49(2):1545–1558, 2010.
Reinhold et al. (2021) J. C. Reinhold, A. Carass, and J. L. Prince. A structural causal model for mr images of multiple sclerosis. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 782–792. Springer, 2021.
Reynaud et al. (2022) H. Reynaud, A. Vlontzos, M. Dombrowski, C. Lee, A. Beqiri, P. Leeson, and B. Kainz. D’artagnan: Counterfactual video generation. MICCAI, 2022.
Ronneberger et al. (2015) O. Ronneberger, P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pages 234–241. Springer, 2015.
Rosenbaum and Rubin (1983) P. R. Rosenbaum and D. B. Rubin. The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1):41–55, 1983.
Rubin (1978) D. B. Rubin. Bayesian Inference for Causal Effects: The Role of Randomization. The Annals of Statistics, 6(1):34 – 58, 1978.
Sanchez et al. (2022a) P. Sanchez, A. Kascenas, X. Liu, A. Q. O’Neil, and S. A. Tsaftaris. What is healthy? generative counterfactual diffusion for lesion localization. IJCAI, 2022a.
Sanchez et al. (2022b) P. Sanchez, J. P. Voisey, T. Xia, H. I. Watson, A. Q. O’Neil, and S. A. Tsaftaris. Causal machine learning for healthcare and precision medicine. Royal Society Open Science, 9(8):220638, 2022b.
Sanchez-Romero et al. (2018) R. Sanchez-Romero, J. Ramsey, K. Zhang, M. R. K. Glymour, B. Huang, and C. Glymour. Causal discovery of feedback networks with functional magnetic resonance imaging. Network Neuroscience, 2018.
Sanchez-Romero et al. (2019) R. Sanchez-Romero, J. D. Ramsey, K. Zhang, and C. Glymour. Identification of effective connectivity subregions. arXiv preprint arXiv:1908.03264, 2019.
Santa Cruz et al. (2021) B. G. Santa Cruz, C. Vega, and F. Hertel. The need of standardised metadata to encode causal relationships: Towards safer data-driven machine learning biological solutions. Proceedings of CIBB, page 1, 2021.
Schrouff et al. (2022) J. Schrouff, N. Harris, O. Koyejo, I. Alabdulmohsin, E. Schnider, K. Opsahl-Ong, A. Brown, S. Roy, D. Mincu, C. Chen, et al. Maintaining fairness across distribution shift: do we have viable solutions for real-world applications? arXiv preprint arXiv:2202.01034, 2022.
Singla et al. (2021) S. Singla, S. Wallace, S. Triantafillou, and K. Batmanghelich. Using causal analysis for conceptual deep learning explanation. In M. de Bruijne, P. C. Cattin, S. Cotin, N. Padoy, S. Speidel, Y. Zheng, and C. Essert, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2021, pages 519–528, Cham, 2021. Springer International Publishing. ISBN 978-3-030-87199-4.
Spirtes et al. (2000) P. Spirtes, C. N. Glymour, R. Scheines, and D. Heckerman. Causation, prediction, and search. MIT press, 2000.
Splawa-Neyman et al. (1990) J. Splawa-Neyman, D. M. Dabrowska, and T. P. Speed. On the Application of Probability Theory to Agricultural Experiments. Essay on Principles. Section 9. Statistical Science, 5(4):465 – 472, 1990.
Valvano et al. (2021) G. Valvano, A. Leo, and S. A. Tsaftaris. Re-using adversarial mask discriminators for test-time training under distribution shifts. Machine Learning for Biomedical Imaging, MICCAI 2021 workshop omnibus special issue, 2021.
Vlontzos et al. (2021a) A. Vlontzos, B. Kainz, and C. M. Gilligan-Lee. Estimating the probabilities of causation via deep monotonic twin networks. arXiv preprint arXiv:2109.01904, 2021a.
Vlontzos et al. (2021b) A. Vlontzos, G. Sutherland, S. Ganju, and F. Soboczenski. Next-gen machine learning supported diagnostic systems for spacecraft. AI for Spacecraft Longevity Workshop at IJCAI, 2021b.
Vlontzos et al. (2022) A. Vlontzos, H. Reynaud, and B. Kainz. Is more data all you need? a causal exploration. arXiv:2206.02409, 2022.
Vowels et al. (2021) M. J. Vowels, N. C. Camgoz, and R. Bowden. D’ya like dags? a survey on structure learning and causal discovery. ACM Computing Surveys (CSUR), 2021.
Wang et al. (2021) R. Wang, P. Chaudhari, and C. Davatzikos. Harmonization with flow-based causal inference. In M. de Bruijne, P. C. Cattin, S. Cotin, N. Padoy, S. Speidel, Y. Zheng, and C. Essert, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2021, pages 181–190, Cham, 2021. Springer International Publishing. ISBN 978-3-030-87199-4.
Yao et al. (2021) L. Yao, Z. Chu, S. Li, Y. Li, J. Gao, and A. Zhang. A survey on causal inference. ACM Transactions on Knowledge Discovery from Data (TKDD), 15(5):1–46, 2021.
Ye et al. (2021a) H. Ye, C. Xie, Y. Liu, and Z. Li. Out-of-distribution generalization analysis via influence function. arXiv preprint arXiv:2101.08521, 2021a.
Ye et al. (2021b) N. Ye, K. Li, L. Hong, H. Bai, Y. Chen, F. Zhou, and Z. Li. Ood-bench: Benchmarking and understanding out-of-distribution generalization datasets and algorithms. CVPR, 2021b.
Yi et al. (2020) K. Yi, C. Gan, Y. Li, P. Kohli, J. Wu, A. Torralba, and J. B. Tenenbaum. Clevrer: Collision events for video representation and reasoning, 2020.
Zapaishchykova et al. (2021) A. Zapaishchykova, D. Dreizin, Z. Li, J. Y. Wu, S. Faghihroohi, and M. Unberath. An interpretable approach to automated severity scoring in pelvic trauma. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 424–433. Springer, 2021.
Zhang et al. (2021) H. Zhang, N. Dullerud, L. Seyyed-Kalantari, Q. Morris, S. Joshi, and M. Ghassemi. An empirical framework for domain generalization in clinical settings. In Proceedings of the Conference on Health, Inference, and Learning, CHIL ’21, page 279–290, New York, NY, USA, 2021. Association for Computing Machinery. ISBN 9781450383592.
Zhang et al. (2022) Y. Zhang, M. Gong, T. Liu, G. Niu, X. Tian, B. Han, B. Schölkopf, and K. Zhang. Adversarial robustness through the lens of causality. ArXiv, abs/2106.06196, 2022.
Zheng et al. (2018) X. Zheng, B. Aragam, P. K. Ravikumar, and E. P. Xing. Dags with no tears: Continuous optimization for structure learning. Advances in Neural Information Processing Systems, 31, 2018.
Zhuang et al. (2021) J. Zhuang, N. Dvornek, S. Tatikonda, X. Papademetris, P. Ventola, and J. S. Duncan. Multiple-shooting adjoint method for whole-brain dynamic causal modeling. In A. Feragen, S. Sommer, J. Schnabel, and M. Nielsen, editors, Information Processing in Medical Imaging, pages 58–70, Cham, 2021. Springer International Publishing. ISBN 978-3-030-78191-0.

[bib.bib1] Adebayo et al. (2022) J. Adebayo, M. Muelly, H. Abelson, and B. Kim. Post hoc explanations may be ineffective for detecting unknown spurious correlation. In International Conference on Learning Representations, 2022. URL https://openreview.net/forum?id=xNOVfCCvDpM.

[bib.bib2] Balke and Pearl (1994) A. Balke and J. Pearl. Probabilistic evaluation of counterfactual queries. In AAAI, 1994.

[bib.bib3] Baniasadi et al. (2022) M. Baniasadi, M. V. Petersen, J. Goncalves, A. Horn, V. Vlasov, F. Hertel, and A. Husch. Dbsegment: Fast and robust segmentation of deep brain structures–evaluation of transportability across acquisition domains. Human Brain Mapping, 2022.

[bib.bib4] Benkarim et al. (2021) O. Benkarim, C. Paquola, B.-y. Park, V. Kebets, S.-J. Hong, R. V. de Wael, S. Zhang, B. T. Yeo, M. Eickenberg, T. Ge, et al. The cost of untracked diversity in brain-imaging prediction. bioRxiv, 2021.

[bib.bib5] Bernhardt et al. (2022) M. Bernhardt, C. Jones, and B. Glocker. Investigating underdiagnosis of ai algorithms in the presence of multiple sources of dataset bias. arXiv preprint arXiv:2201.07856, 2022.

[bib.bib6] Bielczyk et al. (2017) N. Z. Bielczyk, S. Uithol, T. van Mourik, M. N. Havenith, P. Anderson, J. C. Glennon, and K. Buitelaar. Causal inference in functional magnetic resonance imaging. arXiv preprint arXiv:1708.04020, 2017.

[bib.bib7] Budd et al. (2021) S. Budd, E. C. Robinson, and B. Kainz. A survey on active learning and human-in-the-loop deep learning for medical image analysis. Medical Image Analysis, 71:102062, 2021. ISSN 1361-8415.

[bib.bib8] Cabezas et al. (2011) M. Cabezas, A. Oliver, X. Lladó, J. Freixenet, and M. B. Cuadra. A review of atlas-based segmentation for magnetic resonance brain images. Computer methods and programs in biomedicine, 104(3):e158–e177, 2011.

[bib.bib9] Castro et al. (2020a) D. C. Castro, I. Walker, and B. Glocker. Causality matters in medical imaging. Nature Communications, 11(1):3673, Jul 2020a.

[bib.bib10] Castro et al. (2020b) D. C. Castro, I. Walker, and B. Glocker. Causality matters in medical imaging. Nature Communications, 11(1):1–10, 2020b.

[bib.bib11] Chen et al. (2021) R. J. Chen, T. Y. Chen, J. Lipkova, J. J. Wang, D. F. Williamson, M. Y. Lu, S. Sahai, and F. Mahmood. Algorithm fairness in ai for medicine and healthcare. arXiv preprint arXiv:2110.00603, 2021.

[bib.bib12] Chickering (2003) D. M. Chickering. Optimal structure identification with greedy search. J. Mach. Learn. Res., 3(null):507–554, mar 2003. ISSN 1532-4435.

[bib.bib13] Chuang et al. (2022) K.-C. Chuang, S. Ramakrishnapillai, L. Bazzano, and O. Carmichael. Nonlinear conditional time-varying granger causality of task fmri via deep stacking networks and adaptive convolutional kernels. In L. Wang, Q. Dou, P. T. Fletcher, S. Speidel, and S. Li, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2022, pages 271–281, Cham, 2022. Springer Nature Switzerland.

[bib.bib14] Clivio et al. (2022) O. Clivio, F. Falck, B. Lehmann, G. Deligiannidis, and C. Holmes. Neural score matching for high-dimensional causal inference. AISTATS, 2022.

[bib.bib15] Cortes-Briones et al. (2021) J. A. Cortes-Briones, N. I. Tapia-Rivas, D. C. D’Souza, and P. A. Estevez. Going deep into schizophrenia with artificial intelligence. Schizophrenia Research, 2021.

[bib.bib16] da Silva et al. (2020) M. da Silva, K. Garcia, C. H. Sudre, C. Bass, M. J. Cardoso, and E. Robinson. Biomechanical modelling of brain atrophy through deep learning. arXiv preprint arXiv:2012.07596, 2020.

[bib.bib17] DeGrave et al. (2021) A. J. DeGrave, J. D. Janizek, and S.-I. Lee. Ai for radiographic covid-19 detection selects shortcuts over signal. Nature Machine Intelligence, 2021.

[bib.bib18] Ding et al. (2022) H. Ding, J. Zhang, P. Kazanzides, J. Y. Wu, and M. Unberath. Carts: Causality-driven robot tool segmentation from vision and kinematics data. In L. Wang, Q. Dou, P. T. Fletcher, S. Speidel, and S. Li, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2022, pages 387–398, Cham, 2022. Springer Nature Switzerland.

[bib.bib19] Dinh et al. (2017) L. Dinh, J. Sohl-Dickstein, and S. Bengio. Density estimation using real nvp. ICLR, 2017.

[bib.bib20] Fehr et al. (2022) J. Fehr, M. Piccininni, T. Kurth, and S. Konigorski. A causal framework for assessing the transportability of clinical prediction models. medRxiv, 2022.

[bib.bib21] Garcea et al. (2021) F. Garcea, L. Morra, and F. Lamberti. On the use of causal models to build better datasets. In 2021 IEEE 45th Annual Computers, Software, and Applications Conference (COMPSAC), pages 1514–1519. IEEE, 2021.

[bib.bib22] (22) B. Garcia Santa Cruz, A. Husch, and F. Hertel. The effect of dataset confounding on predictions of deep neural networks for medical imaging.

[bib.bib23] Gerstenberg et al. (2021) T. Gerstenberg, N. D. Goodman, D. A. Lagnado, and J. B. Tenenbaum. A counterfactual simulation model of causal judgments for physical events. Psychological review, 128(5):936, 2021.

[bib.bib24] Glymour et al. (2019) C. Glymour, K. Zhang, and P. Spirtes. Review of causal discovery methods based on graphical models. Frontiers in Genetics, 10, 2019. ISSN 1664-8021. doi: 10.3389/fgene.2019.00524. URL https://www.frontiersin.org/article/10.3389/fgene.2019.00524.

[bib.bib25] Goodfellow et al. (2014) I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio. Generative adversarial nets. Advances in neural information processing systems, 27, 2014.

[bib.bib26] Gordaliza et al. (2022) P. M. Gordaliza, J. J. Vaquero, and A. Munoz-Barrutia. Translational lung imaging analysis through disentangled representations. arXiv preprint arXiv:2203.01668, 2022.

[bib.bib27] Grzech et al. (2020) D. Grzech, B. Kainz, B. Glocker, and L. Le Folgoc. Image registration via stochastic gradient markov chain monte carlo. In Uncertainty for Safe Utilization of Machine Learning in Medical Imaging, and Graphs in Biomedical Image Analysis, pages 3–12. Springer, 2020.

[bib.bib28] Haskins et al. (2020) G. Haskins, U. Kruger, and P. Yan. Deep learning in medical image registration: a survey. Machine Vision and Applications, 31(1):1–18, 2020.

[bib.bib29] Hirano et al. (2021) H. Hirano, A. Minagi, and K. Takemoto. Universal adversarial attacks on deep neural networks for medical image classification. BMC medical imaging, 21(1):1–13, 2021.

[bib.bib30] Holzinger et al. (2022) A. Holzinger, M. Dehmer, F. Emmert-Streib, R. Cucchiara, I. Augenstein, J. Del Ser, W. Samek, I. Jurisica, and N. Díaz-Rodríguez. Information fusion as an integrative cross-cutting enabler to achieve robust, explainable, and trustworthy medical artificial intelligence. Information Fusion, 79:263–278, 2022.

[bib.bib31] Huang et al. (2020) B. Huang, K. Zhang, J. Zhang, J. Ramsey, R. Sanchez-Romero, C. Glymour, and B. Schölkopf. Causal discovery from heterogeneous/nonstationary data with independent changes. JMLR, Jun 2020.

[bib.bib32] Huang et al. (2019) Y. Huang, T. Würfl, K. Breininger, L. Liu, G. Lauritsch, and A. Maier. Abstract: Some investigations on robustness of deep learning in limited angle tomography. In H. Handels, T. M. Deserno, A. Maier, K. H. Maier-Hein, C. Palm, and T. Tolxdorff, editors, MICCAI, pages 21–21, Wiesbaden, 2019. Springer Fachmedien Wiesbaden.

[bib.bib33] Jiao et al. (2018) R. Jiao, N. Lin, Z. Hu, D. A. Bennett, L. Jin, and M. Xiong. Bivariate causal discovery and its applications to gene expression and imaging data analysis. Frontiers in Genetics, 9, 2018. ISSN 1664-8021. doi: 10.3389/fgene.2018.00347. URL https://www.frontiersin.org/article/10.3389/fgene.2018.00347.

[bib.bib34] Kamnitsas et al. (2017) K. Kamnitsas, C. Ledig, V. F. Newcombe, J. P. Simpson, A. D. Kane, D. K. Menon, D. Rueckert, and B. Glocker. Efficient multi-scale 3D CNN with fully connected crf for accurate brain lesion segmentation. Medical image analysis, 36:61–78, 2017.

[bib.bib35] Kayser et al. (2020) M. Kayser, R. D. Soberanis-Mukul, A.-M. Zvereva, P. Klare, N. Navab, and S. Albarqouni. Understanding the effects of artifacts on automated polyp detection and incorporating that knowledge via learning without forgetting. arXiv preprint arXiv:2002.02883, 2020.

[bib.bib36] Ke et al. (2022) N. R. Ke, S. Chiappa, J. Wang, J. Bornschein, T. Weber, A. Goyal, M. Botvinic, M. Mozer, and D. J. Rezende. Learning to induce causal structure. 2022.

[bib.bib37] Kingma and Welling (2013) D. P. Kingma and M. Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.

[bib.bib38] Kocaoglu et al. (2018) M. Kocaoglu, C. Snyder, A. G. Dimakis, and S. Vishwanath. Causalgan: Learning causal implicit generative models with adversarial training. In International Conference on Learning Representations, 2018.

[bib.bib39] Kouw et al. (2019) W. M. Kouw, S. N. Ørting, J. Petersen, K. S. Pedersen, and M. de Bruijne. A cross-center smoothness prior for variational bayesian brain tissue segmentation. In A. C. S. Chung, J. C. Gee, P. A. Yushkevich, and S. Bao, editors, Information Processing in Medical Imaging, pages 360–371, Cham, 2019. Springer International Publishing. ISBN 978-3-030-20351-1.

[bib.bib40] Kumar et al. (2022) A. Kumar, A. Hu, B. Nichyporuk, J.-P. R. Falet, D. L. Arnold, S. Tsaftaris, and T. Arbel. Counterfactual image synthesis for discovery of personalized predictive image markers. arXiv preprint arXiv:2208.02311, 2022.

[bib.bib41] Lavin et al. (2021) A. Lavin, C. M. Gilligan-Lee, A. Visnjic, S. Ganju, D. Newman, S. Ganguly, D. Lange, A. G. Baydin, A. Sharma, A. Gibson, et al. Technology readiness levels for machine learning systems. arXiv preprint arXiv:2101.03989, 2021.

[bib.bib42] Li et al. (2021) S. Li, M. Sesia, Y. Romano, E. Candès, and C. Sabatti. Searching for consistent associations with a multi-environment knockoff filter. arXiv preprint arXiv:2106.04118, 2021.

[bib.bib43] Li et al. (2020) Y. Li, A. Torralba, A. Anandkumar, D. Fox, and A. Garg. Causal discovery in physical systems from videos. Advances in Neural Information Processing Systems, 33:9180–9192, 2020.

[bib.bib44] Liu et al. (2021) C. Liu, X. Sun, J. Wang, H. Tang, T. Li, T. Qin, W. Chen, and T.-Y. Liu. Learning causal semantic representation for out-of-distribution prediction. Advances in Neural Information Processing Systems, 34, 2021.

[bib.bib45] Löwe et al. (2022) S. Löwe, D. Madras, R. Zemel, and M. Welling. Amortized causal discovery: Learning to infer causal graphs from time-series data, 2022.

[bib.bib46] Maintz and Viergever (1998) J. A. Maintz and M. A. Viergever. A survey of medical image registration. Medical image analysis, 2(1):1–36, 1998.

[bib.bib47] Mani and Cooper (2000) S. Mani and G. F. Cooper. Causal discovery from medical textual data. In Proceedings of the AMIA Symposium, page 542. American Medical Informatics Association, 2000.

[bib.bib48] Mueller et al. (2021) S. Mueller, A. Li, and J. Pearl. Causes of effects: Learning individual responses from population data. 2021.

[bib.bib49] Nauta et al. (2019) M. Nauta, D. Bucur, and C. Seifert. Causal discovery with attention-based convolutional neural networks. Machine Learning and Knowledge Extraction, 1(1):312–340, 2019.

[bib.bib50] Ouyang et al. (2021) C. Ouyang, C. Chen, S. Li, Z. Li, C. Qin, W. Bai, and D. Rueckert. Causality-inspired single-source domain generalization for medical image segmentation. arXiv preprint arXiv:2111.12525, 2021.

[bib.bib51] Pamfil et al. (2020) R. Pamfil, N. Sriwattanaworachai, S. Desai, P. Pilgerstorfer, K. Georgatzis, P. Beaumont, and B. Aragam. Dynotears: Structure learning from time-series data. In International Conference on Artificial Intelligence and Statistics, pages 1595–1605. PMLR, 2020.

[bib.bib52] Papangelou et al. (2018) K. Papangelou, K. Sechidis, J. Weatherall, and G. Brown. Toward an understanding of adversarial examples in clinical trials. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pages 35–51. Springer, 2018.

[bib.bib53] Pawlowski et al. (2020) N. Pawlowski, D. C. Castro, and B. Glocker. Deep structural causal models for tractable counterfactual inference. NeurIPS, 2020.

[bib.bib54] Pearl (2009) J. Pearl. Causality (2nd edition). Cambridge University Press, 2009.

[bib.bib55] Pölsterl and Wachinger (2021) S. Pölsterl and C. Wachinger. Estimation of causal effects in the presence of unobserved confounding in the alzheimer’s continuum. In A. Feragen, S. Sommer, J. Schnabel, and M. Nielsen, editors, Information Processing in Medical Imaging, pages 45–57, Cham, 2021. Springer International Publishing. ISBN 978-3-030-78191-0.

[bib.bib56] Prosperi et al. (2020) M. Prosperi, Y. Guo, M. Sperrin, J. S. Koopman, J. S. Min, X. He, S. Rich, M. Wang, I. E. Buchan, and J. Bian. Causal inference and counterfactual prediction in machine learning for actionable healthcare. Nature Machine Intelligence, 2(7):369–375, 2020.

[bib.bib57] Ramsey et al. (2010) J. D. Ramsey, S. J. Hanson, C. Hanson, Y. O. Halchenko, R. A. Poldrack, and C. Glymour. Six problems for causal inference from fmri. neuroimage, 49(2):1545–1558, 2010.

[bib.bib58] Reinhold et al. (2021) J. C. Reinhold, A. Carass, and J. L. Prince. A structural causal model for mr images of multiple sclerosis. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 782–792. Springer, 2021.

[bib.bib59] Reynaud et al. (2022) H. Reynaud, A. Vlontzos, M. Dombrowski, C. Lee, A. Beqiri, P. Leeson, and B. Kainz. D’artagnan: Counterfactual video generation. MICCAI, 2022.

[bib.bib60] Ronneberger et al. (2015) O. Ronneberger, P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pages 234–241. Springer, 2015.

[bib.bib61] Rosenbaum and Rubin (1983) P. R. Rosenbaum and D. B. Rubin. The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1):41–55, 1983.

[bib.bib62] Rubin (1978) D. B. Rubin. Bayesian Inference for Causal Effects: The Role of Randomization. The Annals of Statistics, 6(1):34 – 58, 1978.

[bib.bib63] Sanchez et al. (2022a) P. Sanchez, A. Kascenas, X. Liu, A. Q. O’Neil, and S. A. Tsaftaris. What is healthy? generative counterfactual diffusion for lesion localization. IJCAI, 2022a.

[bib.bib64] Sanchez et al. (2022b) P. Sanchez, J. P. Voisey, T. Xia, H. I. Watson, A. Q. O’Neil, and S. A. Tsaftaris. Causal machine learning for healthcare and precision medicine. Royal Society Open Science, 9(8):220638, 2022b.

[bib.bib65] Sanchez-Romero et al. (2018) R. Sanchez-Romero, J. Ramsey, K. Zhang, M. R. K. Glymour, B. Huang, and C. Glymour. Causal discovery of feedback networks with functional magnetic resonance imaging. Network Neuroscience, 2018.

[bib.bib66] Sanchez-Romero et al. (2019) R. Sanchez-Romero, J. D. Ramsey, K. Zhang, and C. Glymour. Identification of effective connectivity subregions. arXiv preprint arXiv:1908.03264, 2019.

[bib.bib67] Santa Cruz et al. (2021) B. G. Santa Cruz, C. Vega, and F. Hertel. The need of standardised metadata to encode causal relationships: Towards safer data-driven machine learning biological solutions. Proceedings of CIBB, page 1, 2021.

[bib.bib68] Schrouff et al. (2022) J. Schrouff, N. Harris, O. Koyejo, I. Alabdulmohsin, E. Schnider, K. Opsahl-Ong, A. Brown, S. Roy, D. Mincu, C. Chen, et al. Maintaining fairness across distribution shift: do we have viable solutions for real-world applications? arXiv preprint arXiv:2202.01034, 2022.

[bib.bib69] Singla et al. (2021) S. Singla, S. Wallace, S. Triantafillou, and K. Batmanghelich. Using causal analysis for conceptual deep learning explanation. In M. de Bruijne, P. C. Cattin, S. Cotin, N. Padoy, S. Speidel, Y. Zheng, and C. Essert, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2021, pages 519–528, Cham, 2021. Springer International Publishing. ISBN 978-3-030-87199-4.

[bib.bib70] Spirtes et al. (2000) P. Spirtes, C. N. Glymour, R. Scheines, and D. Heckerman. Causation, prediction, and search. MIT press, 2000.

[bib.bib71] Splawa-Neyman et al. (1990) J. Splawa-Neyman, D. M. Dabrowska, and T. P. Speed. On the Application of Probability Theory to Agricultural Experiments. Essay on Principles. Section 9. Statistical Science, 5(4):465 – 472, 1990.

[bib.bib72] Valvano et al. (2021) G. Valvano, A. Leo, and S. A. Tsaftaris. Re-using adversarial mask discriminators for test-time training under distribution shifts. Machine Learning for Biomedical Imaging, MICCAI 2021 workshop omnibus special issue, 2021.

[bib.bib73] Vlontzos et al. (2021a) A. Vlontzos, B. Kainz, and C. M. Gilligan-Lee. Estimating the probabilities of causation via deep monotonic twin networks. arXiv preprint arXiv:2109.01904, 2021a.

[bib.bib74] Vlontzos et al. (2021b) A. Vlontzos, G. Sutherland, S. Ganju, and F. Soboczenski. Next-gen machine learning supported diagnostic systems for spacecraft. AI for Spacecraft Longevity Workshop at IJCAI, 2021b.

[bib.bib75] Vlontzos et al. (2022) A. Vlontzos, H. Reynaud, and B. Kainz. Is more data all you need? a causal exploration. arXiv:2206.02409, 2022.

[bib.bib76] Vowels et al. (2021) M. J. Vowels, N. C. Camgoz, and R. Bowden. D’ya like dags? a survey on structure learning and causal discovery. ACM Computing Surveys (CSUR), 2021.

[bib.bib77] Wang et al. (2021) R. Wang, P. Chaudhari, and C. Davatzikos. Harmonization with flow-based causal inference. In M. de Bruijne, P. C. Cattin, S. Cotin, N. Padoy, S. Speidel, Y. Zheng, and C. Essert, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2021, pages 181–190, Cham, 2021. Springer International Publishing. ISBN 978-3-030-87199-4.

[bib.bib78] Yao et al. (2021) L. Yao, Z. Chu, S. Li, Y. Li, J. Gao, and A. Zhang. A survey on causal inference. ACM Transactions on Knowledge Discovery from Data (TKDD), 15(5):1–46, 2021.

[bib.bib79] Ye et al. (2021a) H. Ye, C. Xie, Y. Liu, and Z. Li. Out-of-distribution generalization analysis via influence function. arXiv preprint arXiv:2101.08521, 2021a.

[bib.bib80] Ye et al. (2021b) N. Ye, K. Li, L. Hong, H. Bai, Y. Chen, F. Zhou, and Z. Li. Ood-bench: Benchmarking and understanding out-of-distribution generalization datasets and algorithms. CVPR, 2021b.

[bib.bib81] Yi et al. (2020) K. Yi, C. Gan, Y. Li, P. Kohli, J. Wu, A. Torralba, and J. B. Tenenbaum. Clevrer: Collision events for video representation and reasoning, 2020.

[bib.bib82] Zapaishchykova et al. (2021) A. Zapaishchykova, D. Dreizin, Z. Li, J. Y. Wu, S. Faghihroohi, and M. Unberath. An interpretable approach to automated severity scoring in pelvic trauma. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 424–433. Springer, 2021.

[bib.bib83] Zhang et al. (2021) H. Zhang, N. Dullerud, L. Seyyed-Kalantari, Q. Morris, S. Joshi, and M. Ghassemi. An empirical framework for domain generalization in clinical settings. In Proceedings of the Conference on Health, Inference, and Learning, CHIL ’21, page 279–290, New York, NY, USA, 2021. Association for Computing Machinery. ISBN 9781450383592.

[bib.bib84] Zhang et al. (2022) Y. Zhang, M. Gong, T. Liu, G. Niu, X. Tian, B. Han, B. Schölkopf, and K. Zhang. Adversarial robustness through the lens of causality. ArXiv, abs/2106.06196, 2022.

[bib.bib85] Zheng et al. (2018) X. Zheng, B. Aragam, P. K. Ravikumar, and E. P. Xing. Dags with no tears: Continuous optimization for structure learning. Advances in Neural Information Processing Systems, 31, 2018.

[bib.bib86] Zhuang et al. (2021) J. Zhuang, N. Dvornek, S. Tatikonda, X. Papademetris, P. Ventola, and J. S. Duncan. Multiple-shooting adjoint method for whole-brain dynamic causal modeling. In A. Feragen, S. Sommer, J. Schnabel, and M. Nielsen, editors, Information Processing in Medical Imaging, pages 58–70, Cham, 2021. Springer International Publishing. ISBN 978-3-030-78191-0.

A Review of Causality for Learning Algorithms in Medical Image Analysis

Athanasios Vlontzos¹, Daniel Rueckert^2,1, Bernhard Kainz^3,1

1: Imperial College London, 2: TU Munchen, 3: FAU Erlangen-Nurnberg

Publication date: 2022/11/30

https://doi.org/10.59275/j.melba.2022-4gf2

Abstract

1 Introduction